Goal: come as close as you can to the finish line without going over.
How can you possibly come any closer to the finish line than this group?
Oh. My. Goodness. This group of brilliant students got as close to the line as I have ever seen!
|
Racing Day in Algebra 1 Goal: come as close as you can to the finish line without going over. How can you possibly come any closer to the finish line than this group? Wait for it. Wait for it. Oh. My. Goodness. This group of brilliant students got as close to the line as I have ever seen! Congratulations Thomas. That's a photo finish if I ever saw one.
0 Comments
Right off the bat, let me say that I like trig. Or at least I like all the triangles and the easy applications for finding all sorts of lengths. Students in my classes generally like that too. What they find difficult, however, is translation of trigonometric functions. I mean, who looks at y = a*sin([p/(2pi][x-h])+k and says "ooooh I want to do that"? My students initially look at that and panic. You think I'm kidding. This year I hope to change that--I'm stressing transformations for every family of functions we look at rather than limiting it to the chapter dealing with transformations of functions. Those of you with access to Desmos think that's easy. Without student devices I can tell you it's not. I'm also introducing trigonometry by embedding it in the unit circle. If all of the triangles we look at are always brought back to the circle, then all of a sudden the Law of Cosines isn't such a big deal. Shifting functions up, down, left, and right is less scary (I hope). Anyway, that's all to say we starting looking at trigonometry today by playing with hula hoops. We started the class talking about what students remembered about trigonometry--just to get the proverbial wheels turning. They started off slow but then started picking up steam. Then I threw a stick into the spokes: we're going to start talking about trigonometry by looking at circles. We watched the following video: Me: If you were the person recording this video, what would the graph of your experience look like? Guess. Try to sketch it. Student1: How do we graph that? Student2: What are the variables? Me: So you have to identify your independent and dependent variables? (I probably gave too much away there). Student3: Time! Student4: Height? Student2: Are we assuming constant speed? Me: Sure, I think we can make that assumption. Students gave a lot of triangle-looking mountains as graphs. Brilliant. Me: We're going to refine our ideas by making our own Ferris Wheel out of a hula hoop. *cue student rejoicing*
We ran out of time to formalize what I wanted to talk about with them. Finishing the questions on the lab/worksheet was homework. The next day we started class by having students show their graphs. Some student had graphs looking kind of like a bell curve and others had graphs looking like a sine curve. They quickly came to the conclusion that this difference was due to where people started measuring from--either halfway up or from the bottom. Me: So if trigonometry is about triangles, where are the triangles in our circle? Enter Geogebra and interactive websites:
These led to some great conversations about the geometric nature of sine, cosine, and tangent (not to mention cosecant, secant, and cotangent). Sine is the vertical distance of a point on the circle above the x-axis. Cosine is the horizontal distance of a point on the circle from the y-axis. Tangent is the length of the tangent through the point on the circle to the x-axis. Then we talk about ratios, SohCahToa, and solving triangles using neat stuff like: Introducing trig this way adds extra day to the crazy end of the year I-can't-believe-we-had-more-than-10-snow-days blitz to try to cover all the standards. What I hope is that it deepens student understanding and cuts down on the number of days we need to review these concepts.
We explored exponential functions in Algebra 2 recently. I had planned on using the NCTM Illuminations lesson: Too Hot to Handle Too Cold to Enjoy since this past summer. However, as I've become more comfortable doing experiments in my classroom and gotten better at creating my own investigations I decided to steal the idea and make it my own.
I introduced the experiment talking about the McDonald's lawsuit back in the 1990's over a elderly lady getting burned by a cup of coffee. We told some stories and ended up discussing that once coffee is 120 degrees, it's cold enough to not scald you and hot enough to still enjoy. I ladled out water to the groups and they set to work collecting temperature data based on the amount of time that had passed since they first started measuring. Things didn't go well--or at least as well as I had hoped. In the picture below, you can see the tools the students were working with. The thermometer was hard for them to read accurately. As a result, several groups got data that was pretty much linear. Once the students started in on the process of modeling the data, I had to make a quick decision. I hadn't planned on the data showing up linear and students were asking me what kind of model I wanted. I chose to have them make the model they though best fit their data. Here's some samples of student work. Here we had a great discussion about how well the model fits the data AND the situation. All but one of my groups went for an exponential decay model. However, all but one of those groups got the model wrong. They did well enough finding growth factors and starting values but they didn't take into account the horizontal asymptote for an exponential decay function; it's always at y=0. This means for all of the above functions, when we made a scatterplot on our calculators and graphed our equation at the same time, the equation went down much faster than the data--even when using exponential regression. Then the group below presented. They realized the horizontal asymptote needed to be at room temperature so they looked at the thermostat in my room. Then they proceeded to subtract 70 degrees from each of their data points before creating an equation. After finding an equation, they translated the equation back up by 70 degrees. Brilliant!
 I absolutely love it when kids are out of their seats in my class... and on task. There was a point in class today where almost all my students were laying on the floor trying to figure out the height of the ball bounce. How cool is that? The lesson is pretty basic. I wrote up the lesson requirements on the board (see picture below). I'm not proud of it but it's all I had today. Note: even though we've been doing experiments all year, Algebra 1 still needs the suggestion to make a table; thankfully Algebra 2 does not. Gathering Data: For the record, I would like to say that Freshman are awful at measurement. No matter how much we talk about precision, these kids coudn't get a correct height if their grade depended on it (it doesn't by the way). For all of our experiments/activities we measure in centimeters. Some of their measurements were at least 15 cm off. Really? When analyzing the data, groups were pretty quick to realize that picking two random points to find the multiplier wasn't all that accurate. Several students suggested finding the multiplier between each successive bounce and averaging them; I felt like a proud parent. Then they proceeded to make linear equations using the multiplier like it was the slope; I no longer felt proud. We've still got work to do but at least we're having fun doing it. Things have been more than a bit busy up in my neck of the woods. I feel like I'm doing good just to keep getting the kids out of their seats. Deep in my heart I know there must be a good question I can ask at the beginning which will elicit curiosity; I just didn't have the time to think of one. I'm all ears to those of you who have done this before. Luckily for me, playing with balls during math class was enough of a motivator for the students.
Embracing rich contexts, complex tasks and experiments in Algebra 1 and 2 One teacher's story of moving towards inquiry-based learning and peer collaboration in the math classroom. Yesterday I presented at the Math In Action conference at Grand Valley State University. Below are my notes on the presentation and a pdf version of my PowerPoint (which means the videos don't show up).
Teacher Cred
I want to start out with some pictures of my classroom from this past year. My goal in showing you these isn’t so that you think I’m some wonderful teacher; it’s to give weight to what I’m saying. If I can do it, you can do it. Several years back, I went to Western Michigan to get my Master’s degree in math education. When confronted with the research, it’s not hard to see the value in inquiry-based learning coupled with rich contexts in the math classroom... ___________________ (read more) ______________________ I keep trying to push my kids towards modeling. It's not near as easy as it sounds. Maybe my students are different; they need to do experiments over, and over, and over again. This time we made spaghetti bridges and found how many washers it took to break them. We wondered about the relationship was between the number of spaghetti pieces and the amount of weight. (Sorry, I didn't get any pictures of student work for this one). It turns out the relationship is really close to linear. I was proud of how well my students interpreted the data. Several groups had data like: x| 1 | 2 | 3 | 4 | 5 | y| 3 | 6 | 8 | 8 | 14 | Some realized their problem right when looking at the data. Some needed to graph it first. It did this teacher's heart proud to hear students saying to each other: "I think we need to redo this one." or "This doesn't look right, it should keep going up but it doesn't. Let's try it again." At this point in the year, we've gotten really good at interpreting and extending graphs. But I still have a couple of kids struggling with the jump in abstraction when I ask them to make an equation for our data. It's been almost 6 months and I still have kids wanting me to just tell them the answer. I keep reminding myself: ask a question back. I don't show the kids regression until Algebra 2, so they generally attack it one of two ways: 1) They make a line of best fit, pick two points and create an equation (which is my objective for this lesson). -or- 2) They find the average rate of change from the table and a) surmise that no weight will be required to break 0 pieces of spaghetti, putting the y-intercept at 0 or b) they go backwards in the table with their average rate of change and find y when x=0.
This activity went way better than I thought it would. This summer I paged through my textbooks accompanying resources and found an activity suggesting using soup cans, centimeter cubes, water, and rulers to introduce slope-intercept form. My initial reaction was "you're kidding right?". It seemed like a good activity but giving groups of freshman open containers of water sounded like an invitation to several very wet students and multiple detentions. I filed it away, just in case, with no real intention of coming back to it. After a little over a semester of intentionally including multiple experiments every chapter, I wasn't nearly as intimidated when this file stared back at me from my chapter outline last week. I printed out the book's worksheet, gathered some resources for the next day and went home. The morning of, I decided to rework the task a bit (a have both the original and my file at the end of this post). The students did swimmingly. Every student was on task for most of the period. The class did well seeing the relationships between the initial height of the water and the y-intercept as well as between the number of cubes added and the rate of change. When I do this again next year, I'm going to gather some different containers beforehand. Glass worked better than metal containers because the water level was much easier to read. So, I think I'll use some salsa jars, big fat canning jars, and some of the baby food jars from my house (maybe even the plastic Gerber ones will work). Goodness knows I've got enough of those laying around. This is my counter after class. The science teacher was so proud of me.
The setup: How many of you have ever been bungee jumping? (No hands) How many of you want to go bungee jumping? (6 or 7 hands and a whole lot of excited responses of "that would be so cool" or "I don't want to die before I can drive") Today, we're going to do some research for a bungee jump. What do you think are some important questions to ask before you step off the cliff? (Students almost always mention the strength of the bungee cord, how long it is, how much you weigh, and whether or not you have a death wish) Do you think there is a relationship between those things? Does it matter how much you weigh? How much does it matter? Here's our bungee jumper. (Show students the paper clamp with some washers attached) We don't want to send a real person down while we're experimenting because it'd be a shame to kill someone just to gather data. Your groups will use our state-of-the-art bungee apparatus to figure out the relationship between how much the bungee cord stretches based on the weight of the person. Demo: Hand out student worksheets. Demonstrate how to and how not to drop the bungee apparatus and gather data. Let 'em loose: Reconvene: I often start by having student groups present their graphs and lines of best fit. We compare and contrast group work. We talk about what we like and might do differently. Then we shift the conversation to a compare and contrast of what we like about the table, the graph, and the word descriptions. What do we like best? What information does each one present well? What information do we loose in each of them? Then I have them use their graphs to estimate the amount of stretch for 18 and 30 washers. 18 isn't much of an issue. For 30 washers every group need to extend their graph and line of best fit. Plus, we get to have the conversation about the domain of our math model. Will the linear relationship between weight and stretch continue forever? Why or why not? It doesn't take a lot (if any) leading from me for students to see that the stretch will begin to level off at a certain point, or the rubber bands will simply break. I picked up this activity from the 1st edition of Core Plus Course 1 back in 2004. It's similar to the infamous Barbie bungee jump but instead of varying the number of rubber bands, students vary the weight. I like it for a couple of reasons: -it helps students make connections between tables, graphs and words (I don't get into equations on this one those that would be completely doable). -it allows for some great conversations surrounding variables. What does it mean when we say something varies? -once you have the materials, you can do this experiment with virtually no setup from year to year. -it only takes one class period. Materials for each group: 1 Large paper clamp (which will never ever hold papers again), 2 rubber bands, 15 washers (I have a box of old washers I picked up somewhere that I use as weights in multiple experiments throughout the year), 1 centimeter measuring tape (or meter stick).
When teaching proportions or similar figures I generally throw in an example or two of measuring the height of objects you wouldn't normally be able to measure using shadows or various other known distances. Since I've been on my activity/experiment kick, I wanted to go measure shadows to find the heights of trees and telephone poles. However, it's January in Michigan. Nobody wants to go outside and measure shadows, which assumes there will be a sun to cast a shadow. There are sometimes weeks that go by without seeing the sun up here. Enter a brilliant adaptation by Jonathan Claydon for the cannot-go-outside-for-5-months-because-we-live-in-the-midwest group of people. I have my adaptation of it at the bottom of this post. Students start be measuring each member of their group (see below). This measurement is known as the group member's 'real height'. Then groups drift off to the gym to find the height of objects that are too tall to measure easily. I picked three of them: the gym ceiling, the top of the backboard, and the height of the railing on the weight room. Using a ruler, group members find the 'fake height' of a each group member standing next to the too-tall object and the 'fake height' of the object. We found both measurements need to be recorded each time because of differences in how students hold the rulers. After completing our measurements, we went back to our classroom to finish the calculations. Each group member had to find the heights of the objects using their own fake height measurements. Then groups posted a group height for each too-tall object. Lots of good conversations happened when calculated heights didn't agree. Most groups just averaged the calculated heights for each too-tall object. Next, we figured out how we would go about agreeing on the actual height since I don't have the actual measurements myself. With our ceiling calculations, we decided to remove the group's height which was very different before averaging the heights. The class's backboard heights weren't nearly as close. Here we thought the median might be a better descriptor of the 'real height'.
Here again, the 'real heights' were all over the map. They thought the median worked out well last time and wanted to use it again. When we talked about difficulties we encountered, several students said they had difficulty eye-baling the measurements because they couldn't hold their hands steady. When I do this again next year, I plan to hand out a jumbo paper clip to put on each student ruler to serve as a marker for the top measurement. Thanks to http://infinitesums.squarespace.com/commentary/2011/9/30/proportions.html for the idea!
For an activity to do before Christmas vacation, I borrowed this from 8ismyluckynumber.blogspot.com (who borrowed it from sweeneymath.blogspot.com). With a little revision to fit my style and students, we were ready to go--the file is at the bottom of this post. I handed out the project description 2 weeks before attempting it in class together to allow for catapult construction at home. That may have been my 1st mistake (more on that later). A week before the project, students brought in their catapults for a show-and-tell of sorts. The idea was to test the catapults and make any necessary revisions. I had at least one group break their catapult on testing day. The contenders: When I do this project again, I'm going to suggest a couple of designs; none of the plastic spoon catapults lasted through the entirety of the project nor were they accurate enough. Along those same lines, almost all of the catapults broke at some point or other during the project; the question was whether or not they could be fixed. Mr. Sweeny gives step-by-step instructions for creating one. I'll suggest his method next time. Gathering Data: We spent Day 1 in class gathering data about our catapults and calculating equations modeling the flight path of the M&Ms. As with all student created and measured data, the results were less than consistent. I'll definitely have to stress this more next time. Although, because of the errors, we did have some excellent conversations regarding what different aspects of the equations meant and whether or not we thought they were accurate. I had to forcibly move several groups on to the next steps because they were attending to too much precision. Letting the M&Ms fly!
Lab Report This is the first time I've ever had students do a write up of what they did, how they did it and what they learned. The science teacher down the hall was so proud of me. All in all, I'm impressed at the engagement with the material and how well it helps me understand what students understood.
We recently finished up a unit in Physics on Energy--very cool stuff. But the two labs suggested by the book were terrible. I mean awful. How bad were they? They were so bad I felt compelled to create my own. Did I mention I have 6 preps? With all the talk of machines, work, mechanical advantage and efficiency I decided to pick three of the simple machines the book talked about and cobble together a lab on them. While my physics students were doing the lab I thought this would be great for Algebra 2 (or even Algebra 1). None of the math is hard; it's all proportions: work in = work out, or (distance moved)*(force input) = (distance moved)*(force output). Anyway, raid your physics lab for some pulleys, meter sticks, weights and spring scales and have a grand old time of it.
I love using real data in my classes but it's usually easier said than done. I don't have any fancy pants TI-NSpire calculators with little WiFi receivers that transmit data instantaneously to all my students (if anyone wants to buy me a classroom set I would send you a thank you card and a drawing from each of my toddlers). I've tried with regular graphing calculators but it takes almost an entire class period to get the data to everyone. This means I generally don't use student created data as much as I'd like. This year I'm doing something different. I bit the bullet and signed up for the computer cart for a couple days. On day 1, we introduced transformations using Desmos. After playing around with it for 5 mintues we explored different parent functions and their generalized forms: y=x and y=a(x-h)+k, y=x^2 and y=a(x-h)^2+k, and y=2^x and y=2^(x-h)+k. On day 2 we looked at data using Geogebra files I created beforehand (see below). Each of the files is based off the video of a basic event. At this point you need to know I am a complete Geogebra newbie. I had to look up how to get the spreadsheet numbers to show up as points. If I can do it, you can do it. Based on the student questions over these last several days, this is probably the best students have understood the concept of function translations and transformations after the initial introduction.
 I wrote this lesson several years ago for the Kuyers Institute. The question we were trying answer was whether teaching a math lesson could be about more than just the math? Can we talk about social inequality using numbers? What role does math play in convincing people of the rightness or wrongness of an opinion in our society? One of the few times I've been successful with such a lesson is in studying pay inequality between men and women in the U.S.A. I've done this lesson in both Algebra 1 and Algebra 2. I think the older students are better able to delve into the underlying factors (not surprising). 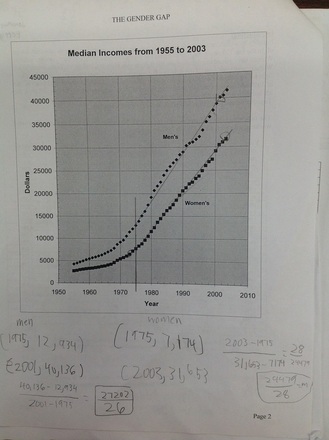 We start by looking at the data from the census bureau: 1955 to 2003. Before beginning group work, we have a discussion about why we use data for median incomes of full-time year round workers. (Women are more likely than men to work part-time in the US and that would skew the data, hence 'full-time year round'. Also, men are more likely to be top earners in the US (think Bill Gates and the like), which would also skew the data, hence 'median'. Then we look for trends in the tables. Almost always students say that men earn more than women and that as the years increase people make more. Then we see if the graphs can help us be more specific (page 2 of the doc). What do you see? Can you use math to describe that? Students suggest exponential curves. We try them and they don't work. Then we talk about cutting off parts of the data. If you cut the data at 1975-ish, it becomes approximately linear. After laying the foundation for the lesson, it's group time. In groups of 3 or 4, students start to work through the questions in the lesson The lesson is divided up into 3 tasks to make for natural discussion breaks as a class for formalization of content. Here's a quick overview: In Task 1 students find equations for both men and women incomes using lines of best fit and two points. Students must also explain what each aspect of the function stands for and whether it is appropriate to predict backwards using the functions. Task 2 tackles linear regression, correlation coefficients and whether our equations have any merit when comparing with current data (I have 2010 incomes in the lesson). Task 3 takes a brief foray into rational functions (cents on the dollar). I couldn't help bring up a conceptual problem by asking students to create a line of best fit for this function as well (it looks linear). However, this yields drastically different results than the findings from the previous tasks. Lovely discussion about why this doesn't work. All in all, it's an interesting lesson that leads to great conversations about the structure of our society, concepts like 'justice' and how we use math to 'prove' our points.
I recently went to the store to purchase light bulbs. The options were a bit overwhelming. Do I buy standard bulbs (incandescent) or energy efficient ones? If I buy energy efficient ones, which kind: LED or Compact Florescent (CFL)? After fruitlessly trying to find 100 watt bulbs with two toddlers in tow for several minutes, I gave up bought some cheap 60 watt incandescent bulbs and decided to figure it our later. When later came I learned the old 100 watt bulbs are no longer sold--hence my difficulty finding them. So, before I have to purchase bulbs again, I decided to figure this thing out. And then I thought to myself, there's a great math lesson in here somewhere! Here's my 1st take at creating a lifetime cost lesson for light bulbs. The MS Word document is 3 pages: incandescent, LED, Compact Fluorescent (CFL). I'm probably going to include it in our system of equations unit.
I'm looking at buying a new washer and dryer. When I started looking at my options online, I couldn't help thinking this would make a great math lesson. Note: I tried getting energy usage information for dryers but apparently they all use about the same amounts. 1) Which washing machine would you purchase? Why? 2) Does the following information change your response?
3) Is there ever a time when the GE washer becomes less expensive than the Kenmore washing machine? If so how long? 4) Given this next option, would you change your mind again or would you keep with your current decision? 5) Use a different solution method to arrive at your conclusion for #3 and #4. Extension: Can you think of another product or area in life where it might be a good idea to pay more at the beginning (on the front end).
|
Andrew Busch
I teach Math at Ralston Valley High School in Arvada, CO. Categories
All
Archives
March 2019
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||