| We start by watching this video: | |
I get all sorts of mountain looking graphs or semi-circles. It's what I want. We are now going to get some intellectual dissonance. After students committed to a graph, we break out the hula hoops. I borrow them for a couple of days from our PE teacher. As an aside, I borrow stuff from the PE teacher and the science teachers all the time. Believe it or not, they are excited that your doing fun stuff in math class. They want you to borrow their stuff. Not kidding.
Most groups finish with the data gathering in 30 minutes or less.
As another aside, I have students start at the bottom, like they are loading onto a Ferris wheel. Technically, this will look like a cosine function with an a-value of -1. However, we're measuring height, which is a sine function. Whatever. In four years of doing this, I've never had it throw students off the scent of the math we're doing.
| Student Handout:
| Basic Teacher stuff, including some links:
| ||||
Q: What do you like or dislike about this graph?
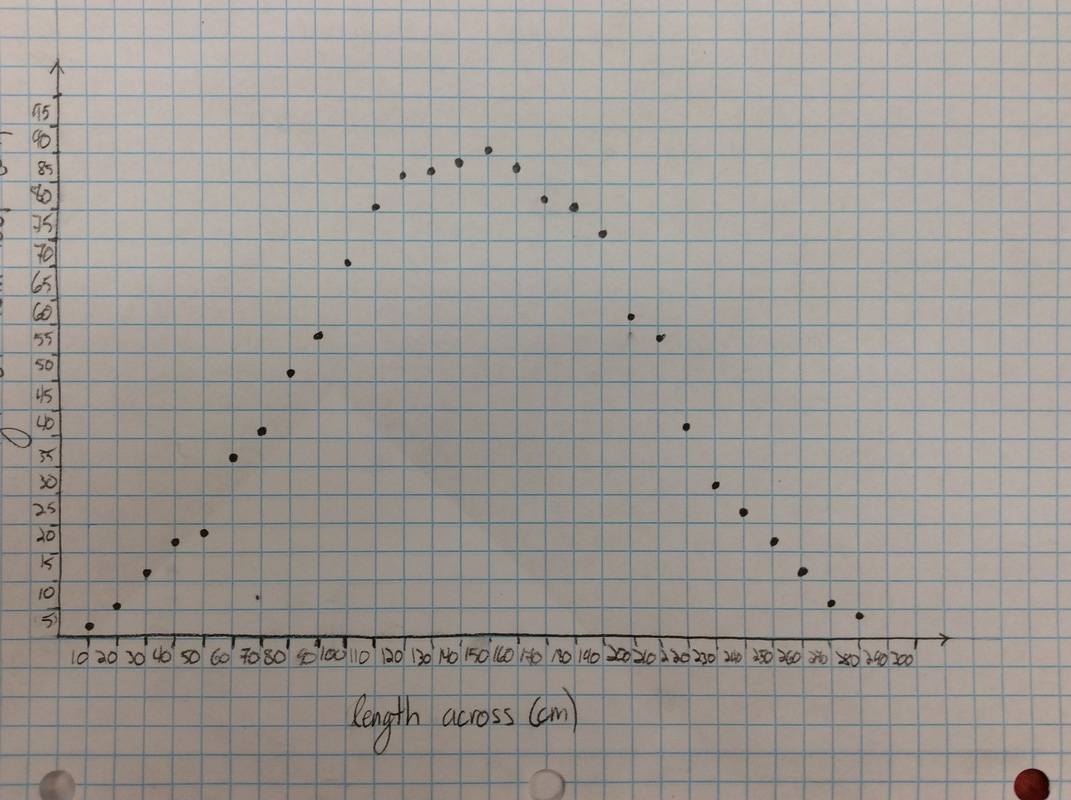
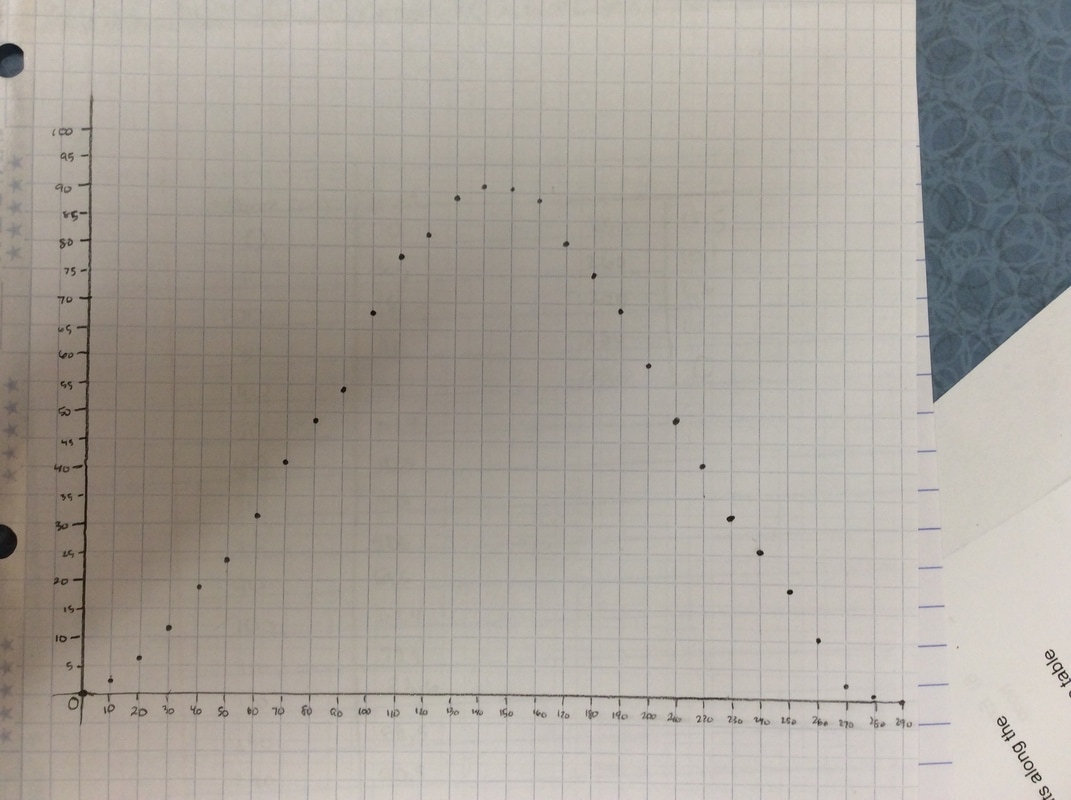
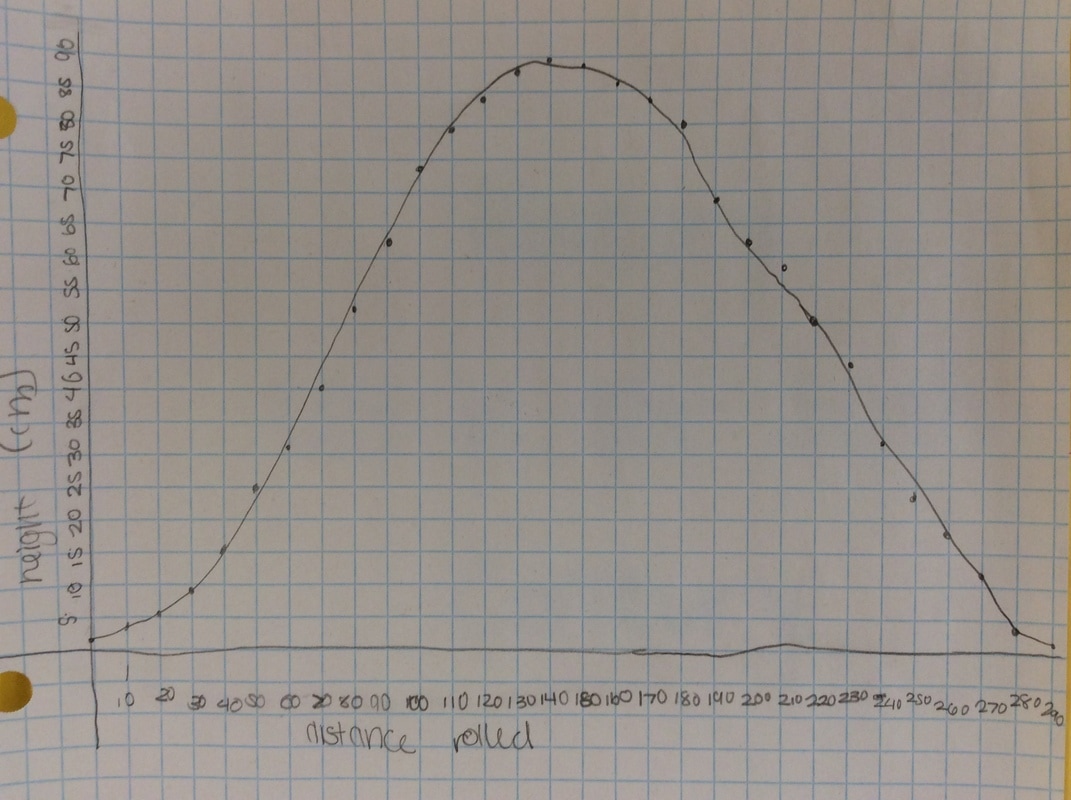
I put the following graph on the screen in response. Students like this one much better. As if almost on cue, some student always says we should connect the points. Then we get to have a good discussion about whether the graph should be continuous or discrete.
The following is the definition of "sine" from Wolphram Alpha. Notice the first part of the definition.
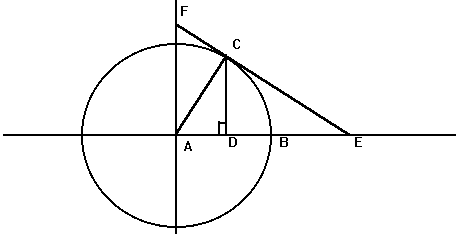
Sine and Cosine as vertical and horizontal distances in the unit circle
http://www.analyzemath.com/unitcircle/unit_circle_applet.html
https://www.mathsisfun.com/algebra/trig-interactive-unit-circle.html
https://www.desmos.com/calculator/v7x6br3w6a
A visualization of Sine and Cosine in the Unit Circle:
(If you want to moving one, click on the link below)
http://i.stack.imgur.com/p8O4P.gif
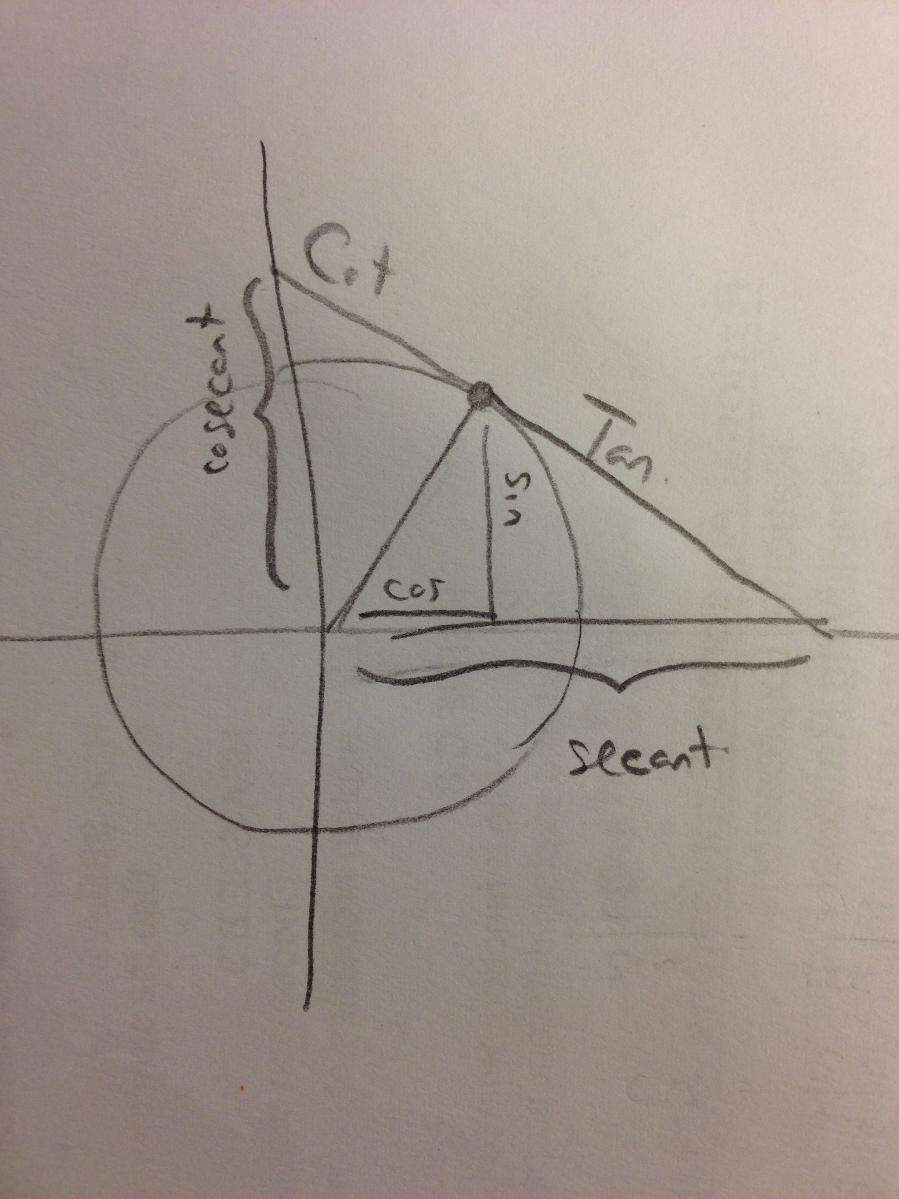
This also helps discuss Cotangent, Secant, and Cosecant when they come up later in the year. They are all actual lengths in the unit circle!
| 17c_exploring_trig_functions.docx |





 RSS Feed
RSS Feed



