|
One word: brilliant. Michael Fenton (@mjfenton) knocks it out of the park talking about technology in education.
0 Comments
Making Math Awesomer: Embracing rich contexts, complex tasks and experiments in Algebra 1 and 2
Teacher Cred I want to start out with some pictures of my classroom from this past year. My goal in showing you these isn't so that you think I’m some wonderful teacher; it’s to give weight to what I’m saying. If I can do it, you can do it. [Pictures are located in the pdf at the bottom of the post if you're interested] Several years back, I went to Western Michigan to get my Master’s degree in math education. When confronted with the research, it’s not hard to see the value in inquiry-based learning coupled with rich contexts in the math classroom. By “inquiry-based” I mean students are investigating mathematical relationships and making conjectures; they’re getting messy with the math. However, shifting my teaching has been a much more difficult process. It’s not that I didn't want to do it; I didn't know where to start. Having the opportunity to teach from Core Plus for a couple of years was helpful but I wasn't trained in the process. Students were frustrated. I was frustrated. Then life happened: my school shifted curriculums, the State changed standards, I bounced around to a couple of different schools (my wife changed jobs, budget cuts, etc), I had kids, etc. I spent years collecting interesting real-world contexts for my lessons but still had this underlying guilt that I wasn't doing it right. My classes did fine compared to other math classes but my students weren't actively engaged in exploring the material. I decided to change that. If I can do this, you can do this. When I started this process I had 6 preps 4 days a week and 7 preps on the other day. I have 3 children 5 and under in my house. This year, I moved to a new state, I use all new/different curriculums… and I teach in a portable. Start small. I don’t use problems or tasks for every topic. I still use direct instruction for some ideas. My initial goal was to incorporate at least 2 rich contexts or activities into each chapter for Algebra 1 and Algebra 2. How to Start the Process Online Resources to get you started: Dan Meyer I know 3-Act tasks are Dan's claim to fame but what I appreciate most about Dan is his reworking of textbook tasks. He also has a mantra I find helpful:
Fawn Nguyen
Geoff Krall
Twitter Twitter has been my best professional development decision in my 14 years of teaching. #MTBoS (Math Twitter Blog-o-Sphere)
#alg2chat #MSMathChat – Mondays 7pm MST
Actual Book: 5 Practices for Orchestrating Productive Mathematics Discussions by Margaret S. Smith and Mark K. Stein. This book has been hands down the best resource I've come across for helping me structure productive discussions in my classes. I’m sure I read something in my masters studies coming close to this, but maybe I just wasn't ready for it. Buy this book!
Suggestions for Organization of Online Resources Evernote and Evernote Web Clipper Organize everything you come across no matter what device or browser you happen to be using. Use tags to help find resources in the future: “Alg2, Quadratic, Activity, PrBL” The Web Clipper is THE best resource because no matter what device I'm using (work computer, laptop, tablet, phone) I can gather the resources I stumble across into one location along with my initial thoughts about how I might use the resource without having to change devices or spend more than 1 minute doing so. Brilliant. Text/Word Document Create a general outline of what you currently do for your course. What topics to you teach? When do you teach them (i.e. chapters or units)? This takes a couple of hours but helps you organize your resources and keeps you from spinning your wheels. Twice a year (or more) go through your accumulated resources in Evernote and find a spot for them to go in your course. Be specific! Find the exact lesson you will replace this with. And if you already have a stellar lesson, don't keep the bad ideas. Only keep the top two or three resources. Sometimes having too many options is just as bad as having no options. Here's a previous blog post I wrote about keeping web resources organized. Your Textbook With a little bit of effort, your textbook can be a good source for rich tasks.
Re-Working a Task Rather than have you listen to me talk about how to rework a task, we're going to try it. We will use the Flashlights and Variation Equations lesson from the Core Plus Mathematics Project, Course 2, pg 10 (used with permission). I would probably use this early in the year with Algebra 2 or late in the year with Algebra 1. What do you notice about this task? Good? Bad? How can we make the task more accessible?
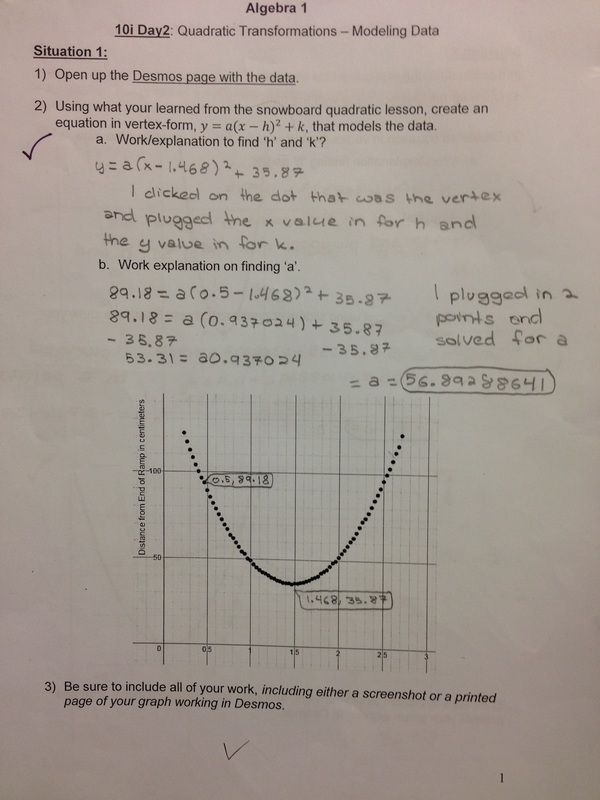
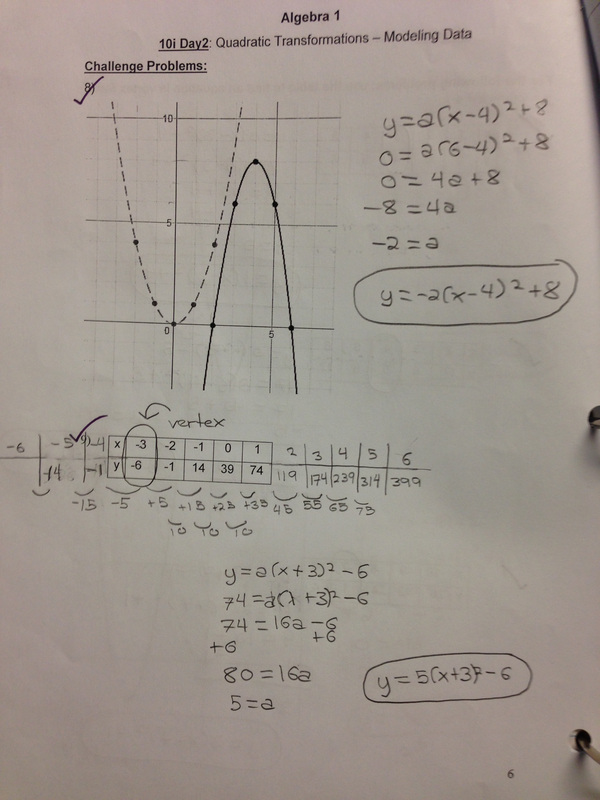
It's not very often something I teach turns out better than expected--but this is it! This year, for the 1st time ever, I successfully taught transformations to Algebra 1 students. Yes, that's right--Algebra 1. I bit the bullet and spent more time than normal designing a unit which forces me to take my classes to the computer lab. I hate the computer lab--mostly because of the sheer amount of time lost to travel and transitions. Maybe someday my students will have computers with them at all times, or I won't be out in the portable trailer park where it takes me just short of forever to go get a chromebook cart. I designed the task for a two-day intensive. On day 1, students use Desmos to match graphs to the paths of skiers and snowboarders. By the end of the period, students mostly understand the vertex form of a quadratic equation: y=a(x-h)^2+k. They are able to describe what the a-value does and how to find 'h' and 'k' without sliders. I made a handout for the students to use during the class period that also includes some practice problems.
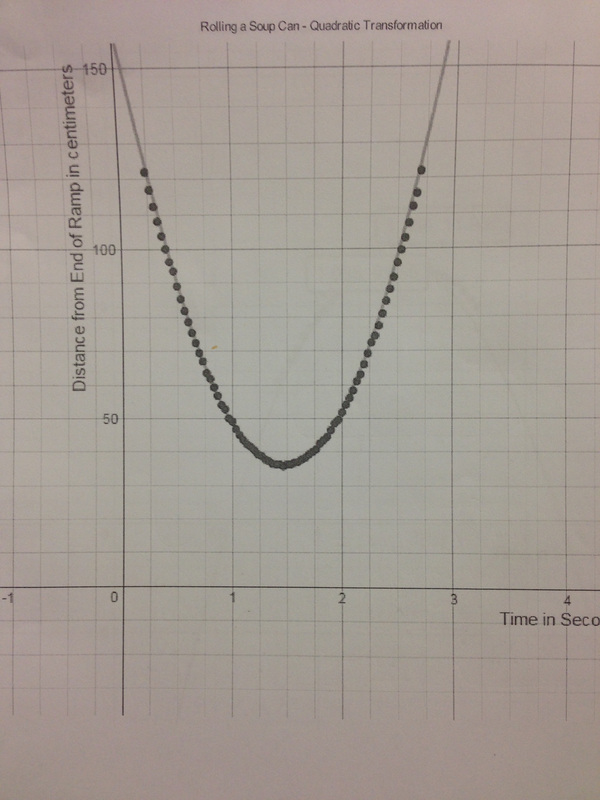
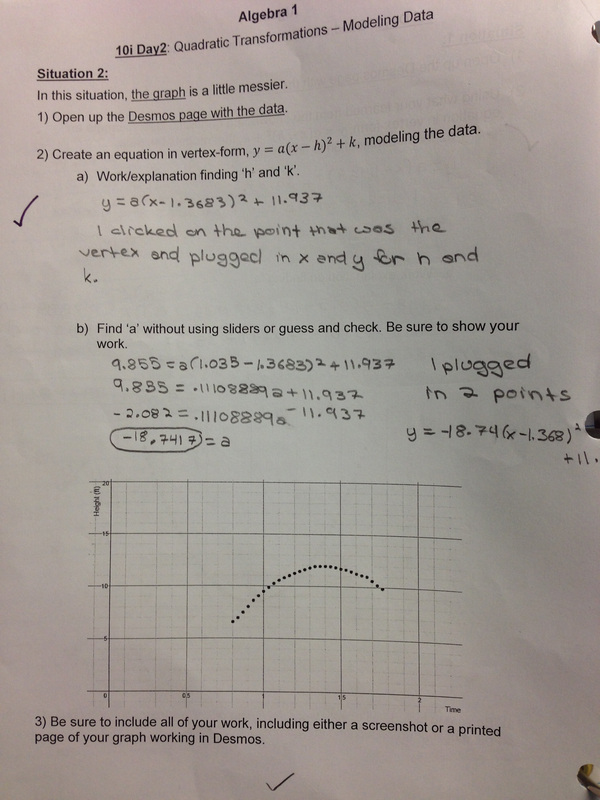
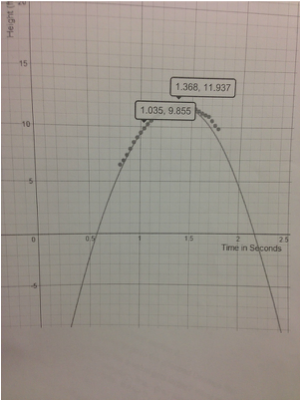
Day 2 is about modeling a situation using the vertex form of the quadratic without using sliders. This means students look at real data, estimate the vertex, then calculate the a-value. They do this in two different situations. Situation 1: Rather than using another projectile example, I used the simple situation of rolling a can up and down a ramp. Below left is a student response on how they fit an equation to the data. Below right is an example of how well the curve fits the data. Situation 2: I use a basketball example here for two reasons: 1) the students dig it, and 2) I didn't do the greatest job tracking the data. Messy data forces student discussions about why the graph of their equation only works for the middle part of the graph but not the edges.
Here's an example of some student work on the practice problems. A huge thanks to John Stevens and Matt Vaudrey for responding to my cry for help on Twitter with insightful comments. Once again the #MTBoS math community demonstrates the benefits of online collaboration.
If you decide to give it a whirl I would love to know how it goes. If you change it up, I'd love to know how so I can tweak it with my students as well. |
Andrew Busch
I teach Math at Ralston Valley High School in Arvada, CO. Categories
All
Archives
March 2019
|
||||||||||||||||||||||||||


 RSS Feed
RSS Feed



