This year I hope to change that--I'm stressing transformations for every family of functions we look at rather than limiting it to the chapter dealing with transformations of functions. Those of you with access to Desmos think that's easy. Without student devices I can tell you it's not. I'm also introducing trigonometry by embedding it in the unit circle. If all of the triangles we look at are always brought back to the circle, then all of a sudden the Law of Cosines isn't such a big deal. Shifting functions up, down, left, and right is less scary (I hope).
Anyway, that's all to say we starting looking at trigonometry today by playing with hula hoops.
Student1: How do we graph that?
Student2: What are the variables?
Me: So you have to identify your independent and dependent variables? (I probably gave too much away there).
Student3: Time!
Student4: Height?
Student2: Are we assuming constant speed?
Me: Sure, I think we can make that assumption.
Students gave a lot of triangle-looking mountains as graphs. Brilliant.
Me: We're going to refine our ideas by making our own Ferris Wheel out of a hula hoop. *cue student rejoicing*
| I had 7 hula hoops so I had 7 groups. Easy. Students got their materials and started to play with the hula hoops. Really? We've been doing experiments all year and today you decide to revert to 3rd grade now? I felt like a broken record going around the room: "let's start working", "do you have a tape measure?", "what point are you measuring on your hula hoop?". In less than 5 minutes kids were mostly settled down and working well. | ||
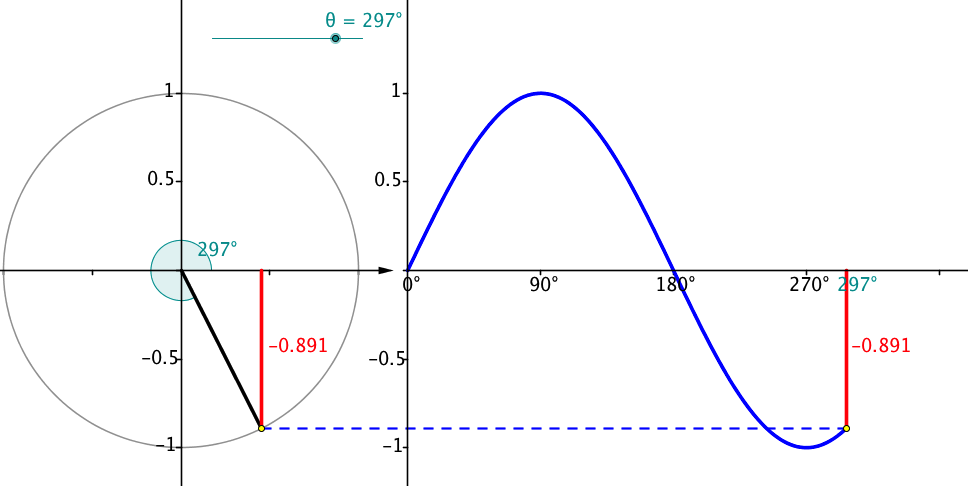
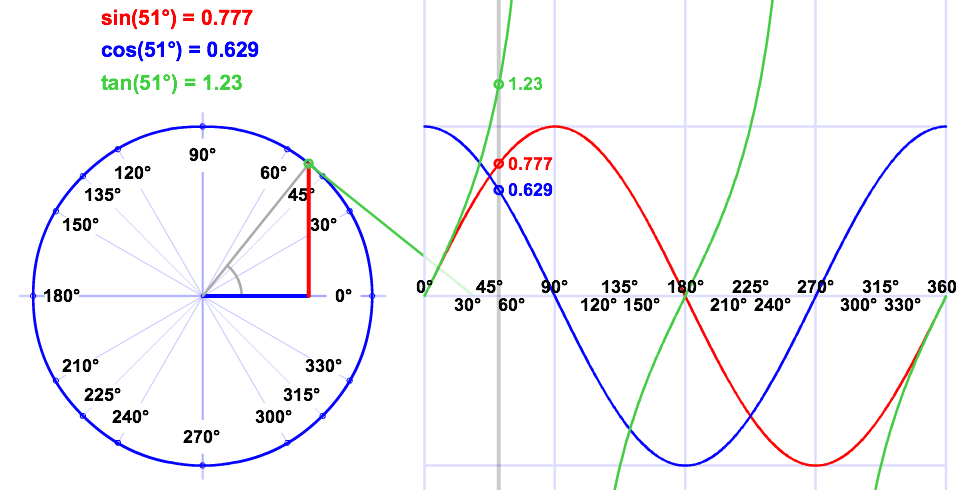
Me: So if trigonometry is about triangles, where are the triangles in our circle?
Enter Geogebra and interactive websites:
| unit_circle_and_the_sine_curve.ggb |
Then we talk about ratios, SohCahToa, and solving triangles using neat stuff like:








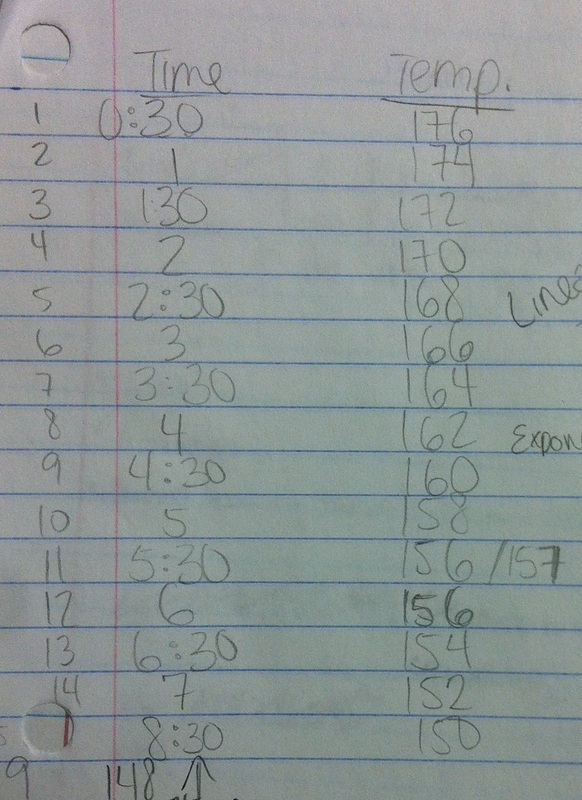



 RSS Feed
RSS Feed



