Andrew Busch

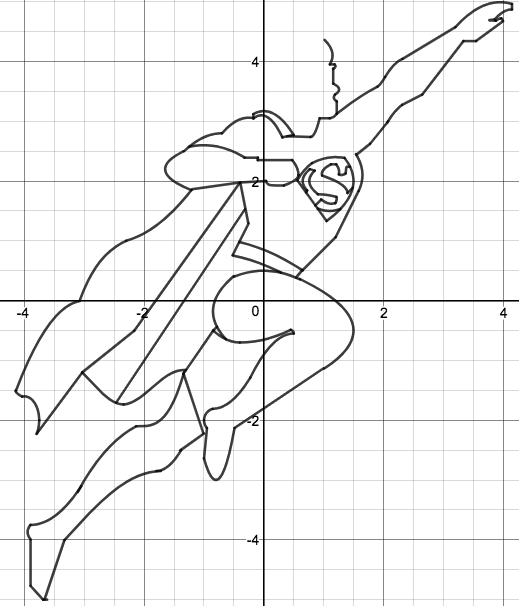
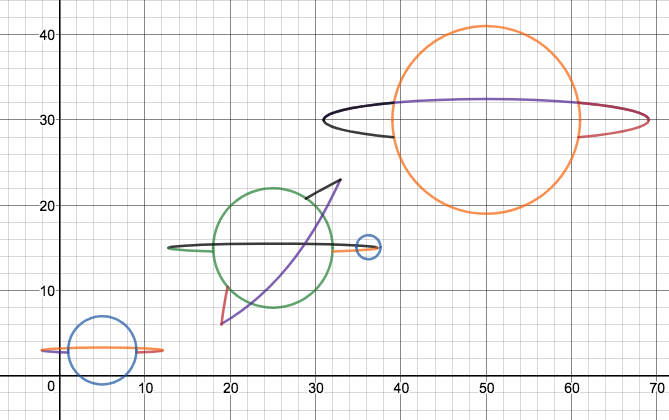
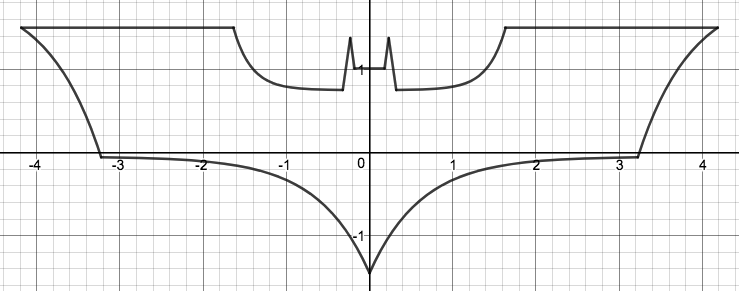
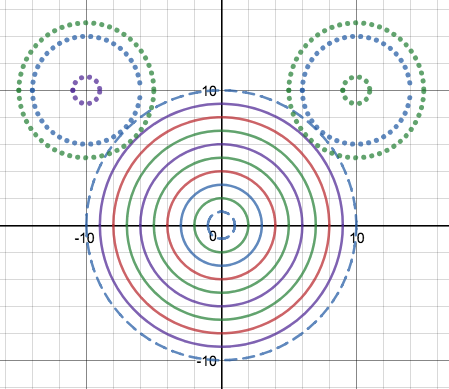
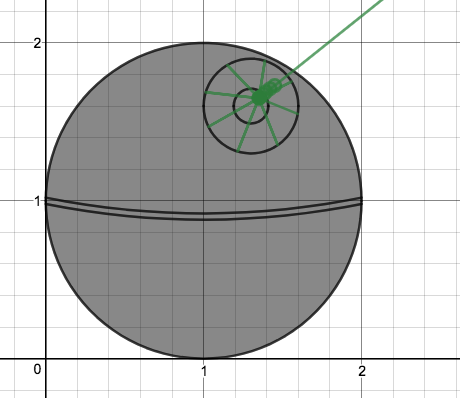
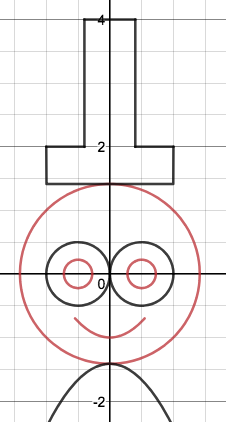
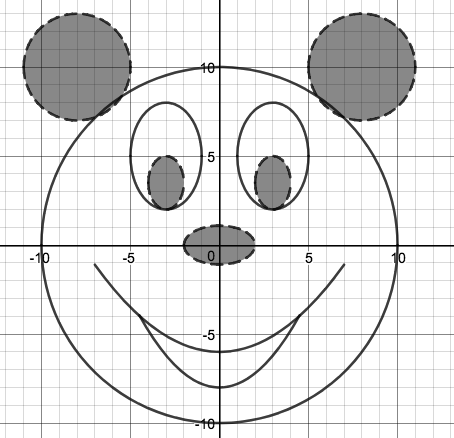
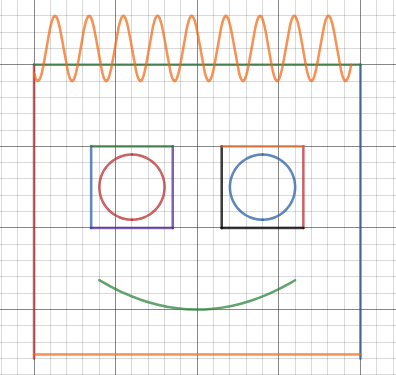
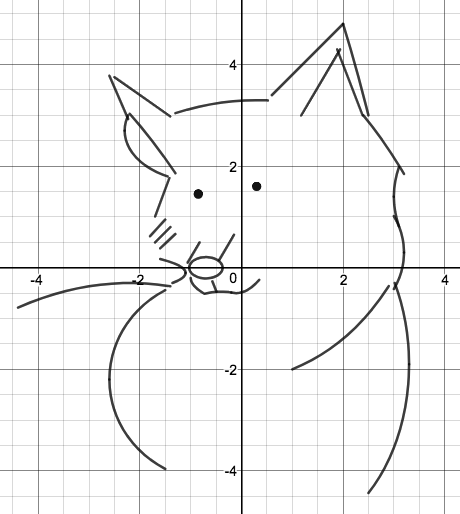
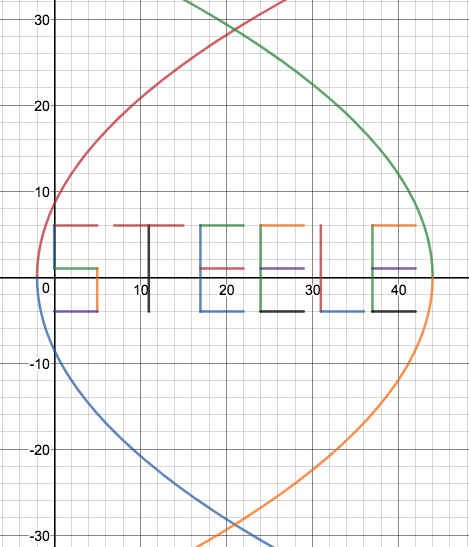
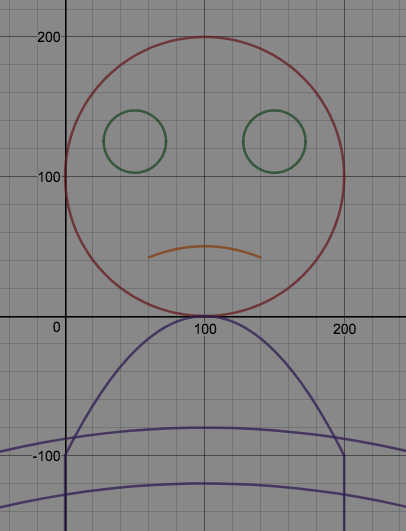
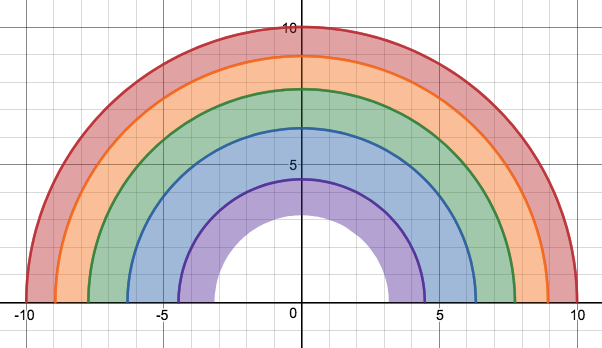
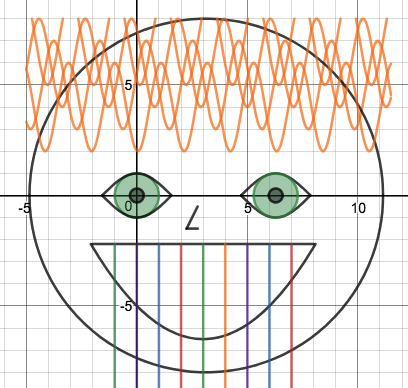
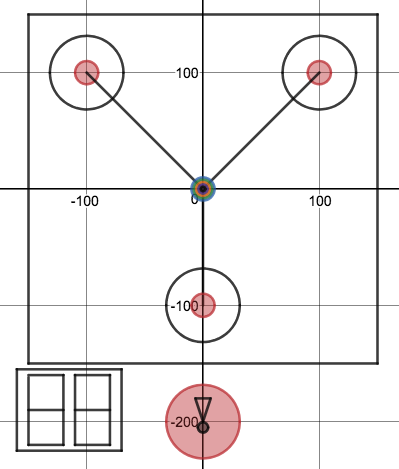
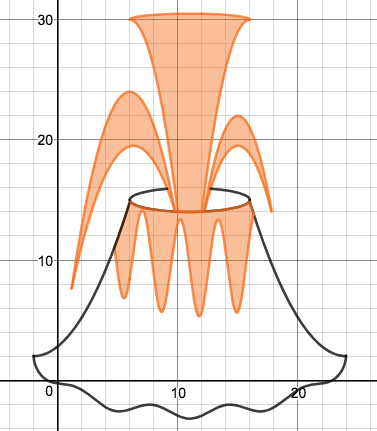
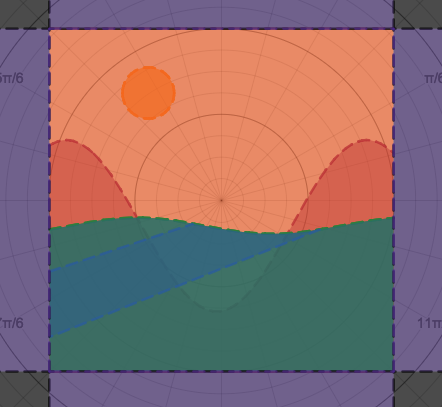
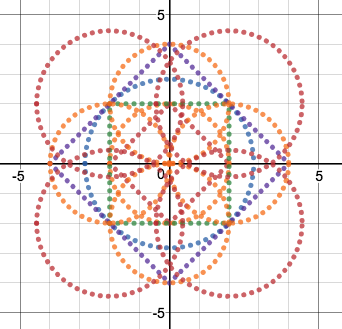
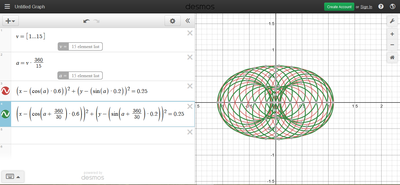
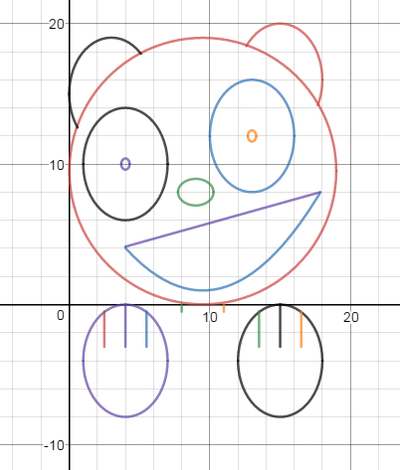
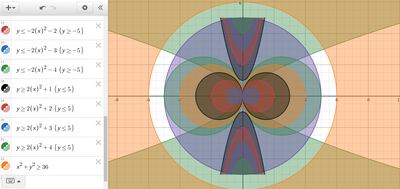
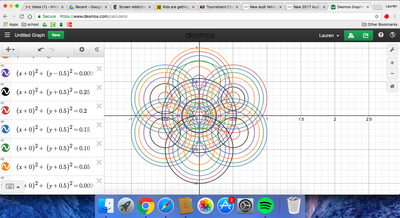
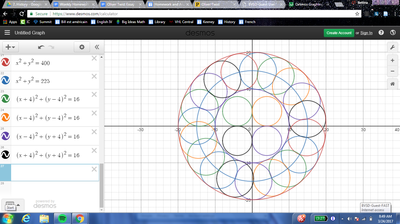
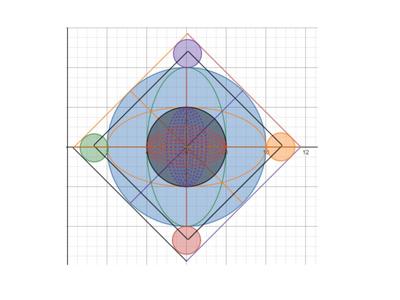
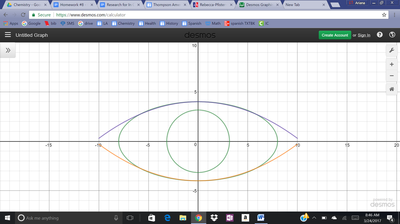
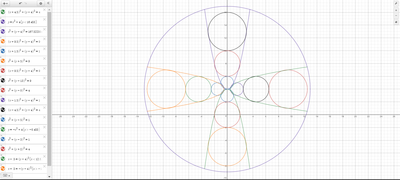
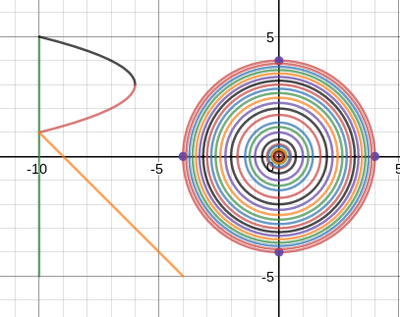
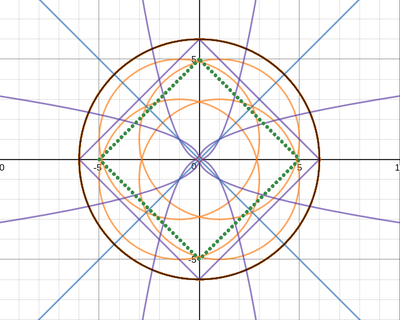
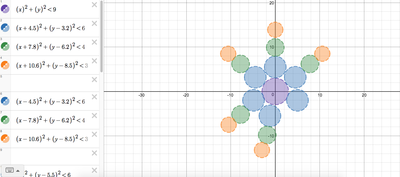
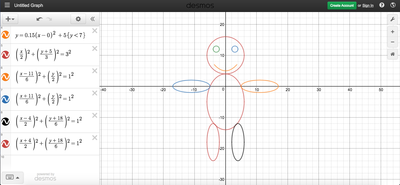
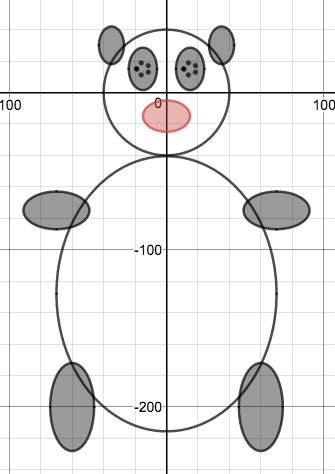
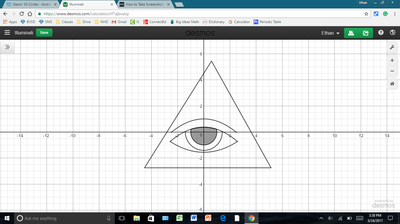
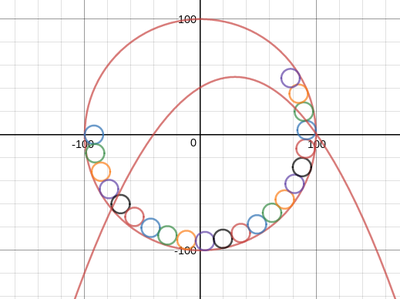
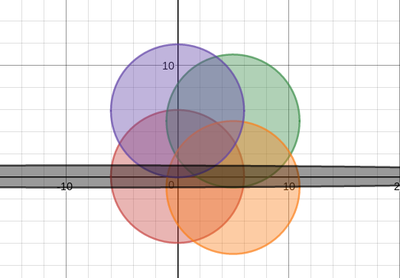
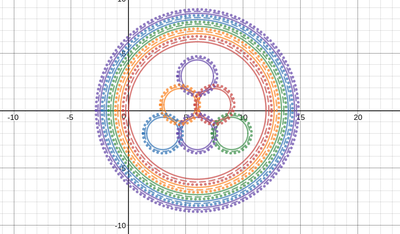
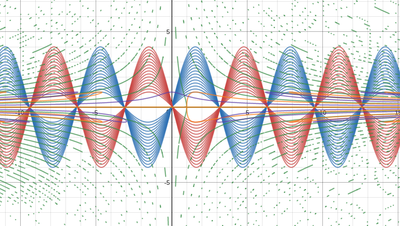
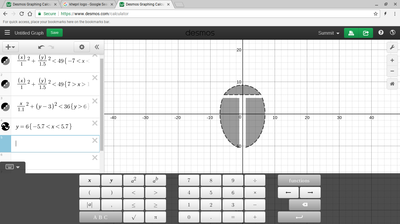
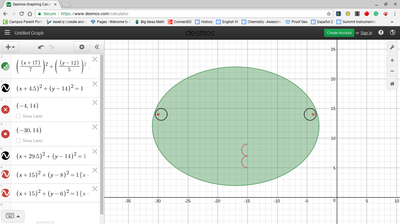
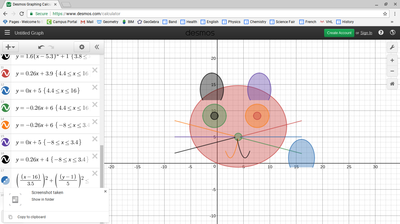
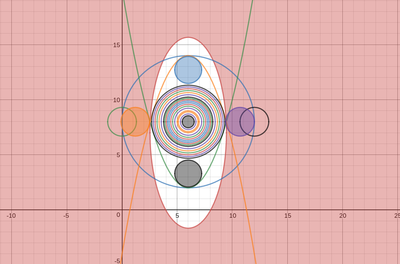
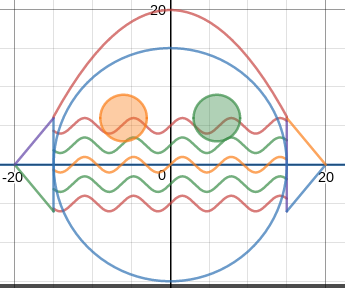
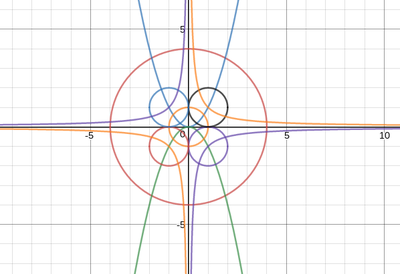
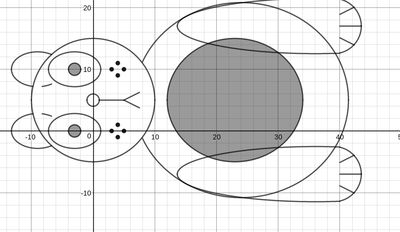
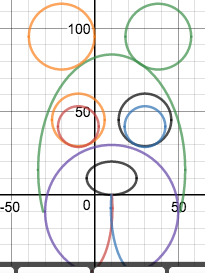
We just finished up our circles unit in Geometry. I had one more day before a long weekend. Rather than jumping into something new, we did a little bit of math art a la Desmos. I gave them a quick directions document with some review of families of functions they might want to explore. Then I set them loose. I gave students a choice whether or not they wanted to work on their drawings after the class period ended. That was not the assignment. Some students decided to go all out!

Are you ready? I don't think you're ready. 

BTW, I linked the pictures to the actual Desmos pages. You're welcome!

The moon revolves around the planet in this one!

I base all of the trigonometric functions/ratios in the unit circle. We use this activity as an anchor for our future discussions about all sorts of things: the graph of sine and cosine, how we create triangles within the circle, and even sine being the distance from the x-axis and cosine the distance from the y-axis.

I overheard multiple conversations between students who noticed the rate of change both sped up and slowed down. They were convinced they were doing it wrong. That's the kind of dissonance I'm looking for!

Here is a complete write up of the lesson.

Original problem by Robert Kaplinsky. I use the problem directly after we learn about special right triangles in Geometry (45-45-90 and 30-60-90). Lot's of great overlap between Algebra and Geometry here. Lot's of great opportunities for students to present different solution methods.

Here's the slide deck and handout I use with my students.

We spent a day working on a fun task from the MARS Team.

Here is the only setup: 

• This diagram shows a circle with one equilateral triangle inside and one equilateral triangle outside.
• Find the exact ratio of the areas of the two triangles. Be convincing in your explanation.

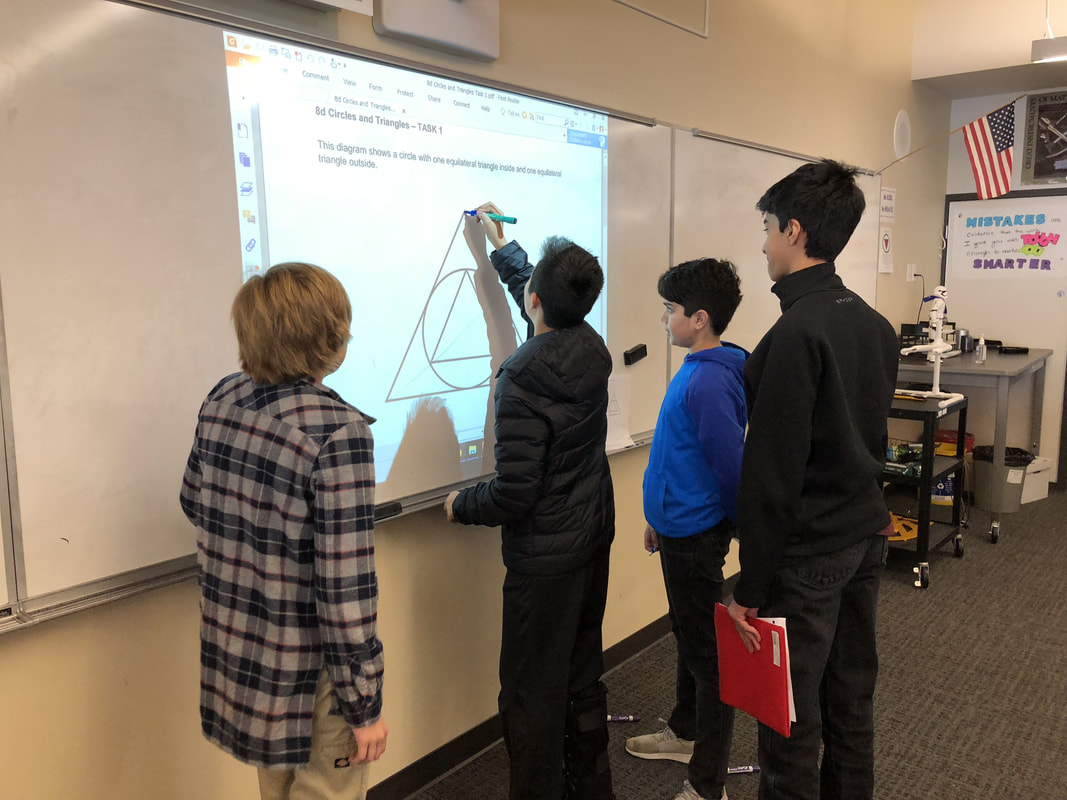
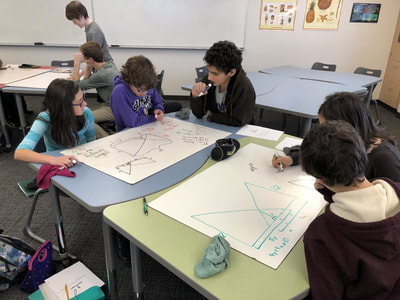
After spending 30 minutes or so working on this problem in groups, we ran out of time. Meh. We planned on starting class the next day talking about our ideas for solution methods. Normally, with two minutes left of class, they line up at the door like cattle. Some of the students weren't done with the problem yet. 

This activity helps students solidify their understanding of the new vocabulary identifying the angles created by a transversal between two lines. To make it a wee-bit more interesting, we also look at transversals across non-parallel lines. 

What to do in Geometry after finishing up our circles unit with one day left before Spring break? Algebra review in the form of art class!

Here's some of the work my students elected to turn in. I gave them one class period to work on it and asked them to turn in whatever they had. If students wanted to do more, they could but it was not required. Hence the varying degrees of completeness. 

I think they did brilliant!

A few years ago I started introducing trigonometry using circles. It started in Algebra 2 and moved down into Geometry. By basing all trig off the unit circle, we make an easy transition from Geometry trig (finding missing sides and angles of triangles) to Algebra 2 trig (sine and cosine functions and transformations). After a couple of years, I'm never going back.

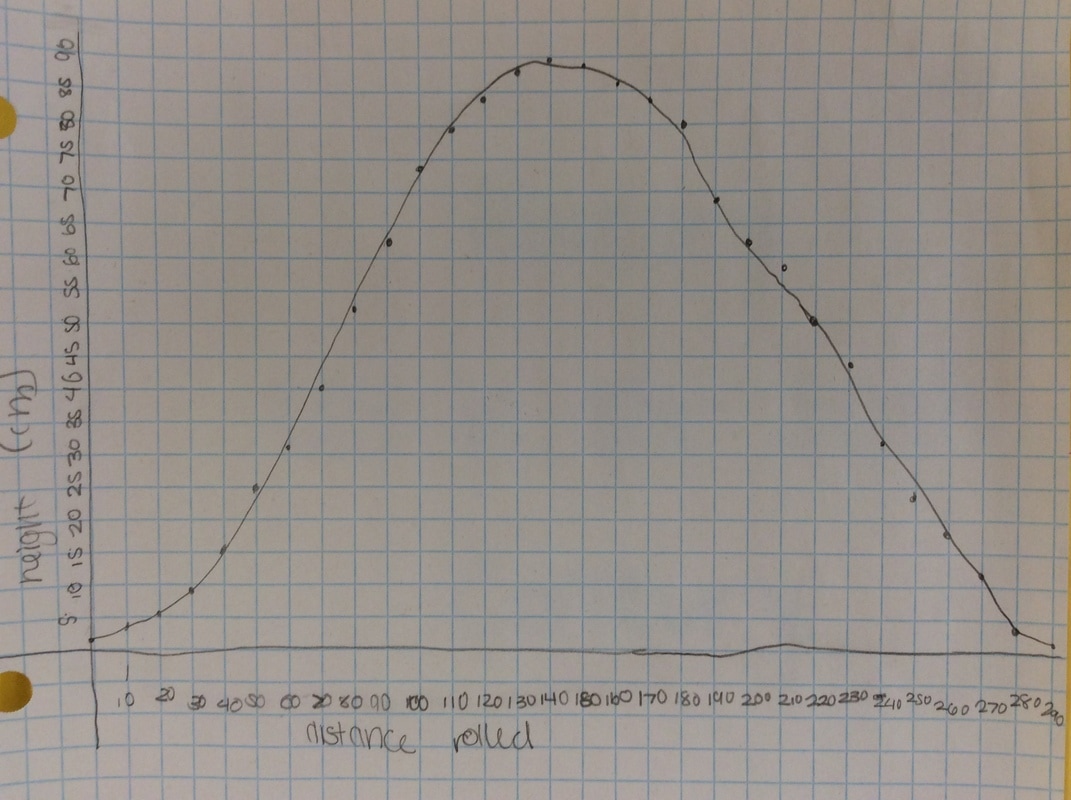
Q: If you were the person taking this video, what would the graph of your height look like? Sketch a graph. 

​I get all sorts of mountain looking graphs or semi-circles. It's what I want. We are now going to get some intellectual dissonance. After students committed to a graph, we break out the hula hoops. I borrow them for a couple of days from our PE teacher. As an aside, I borrow stuff from the PE teacher and the science teachers all the time. Believe it or not, they are excited that your doing fun stuff in math class. They want you to borrow their stuff. Not kidding.

We give a two-minute talk through regarding how we are going to collect data. Something like: Put some tape on the hula hoops and put a dot on the side of the hula hoop. This dot is you. Throughout the experiment, you will always measure the height of the dot. You will roll the hula hoop 10 cm and then measure the height of the dot. In cm. When you get to the end of your meter stick, keep your fingers on the bottom point and slide it back to the beginning of the meter stick. Do this for one complete revolution of the hula hoop/ferris wheel.

Most groups finish with the data gathering in 30 minutes or less. 

As another aside, I have students start at the bottom, like they are loading onto a Ferris wheel. Technically, this will look like a cosine function with an a-value of -1. However, we're measuring height, which is a sine function. Whatever. In four years of doing this, I've never had it throw students off the scent of the math we're doing. 

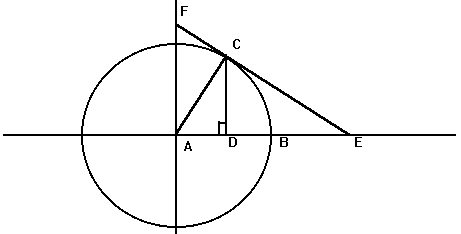
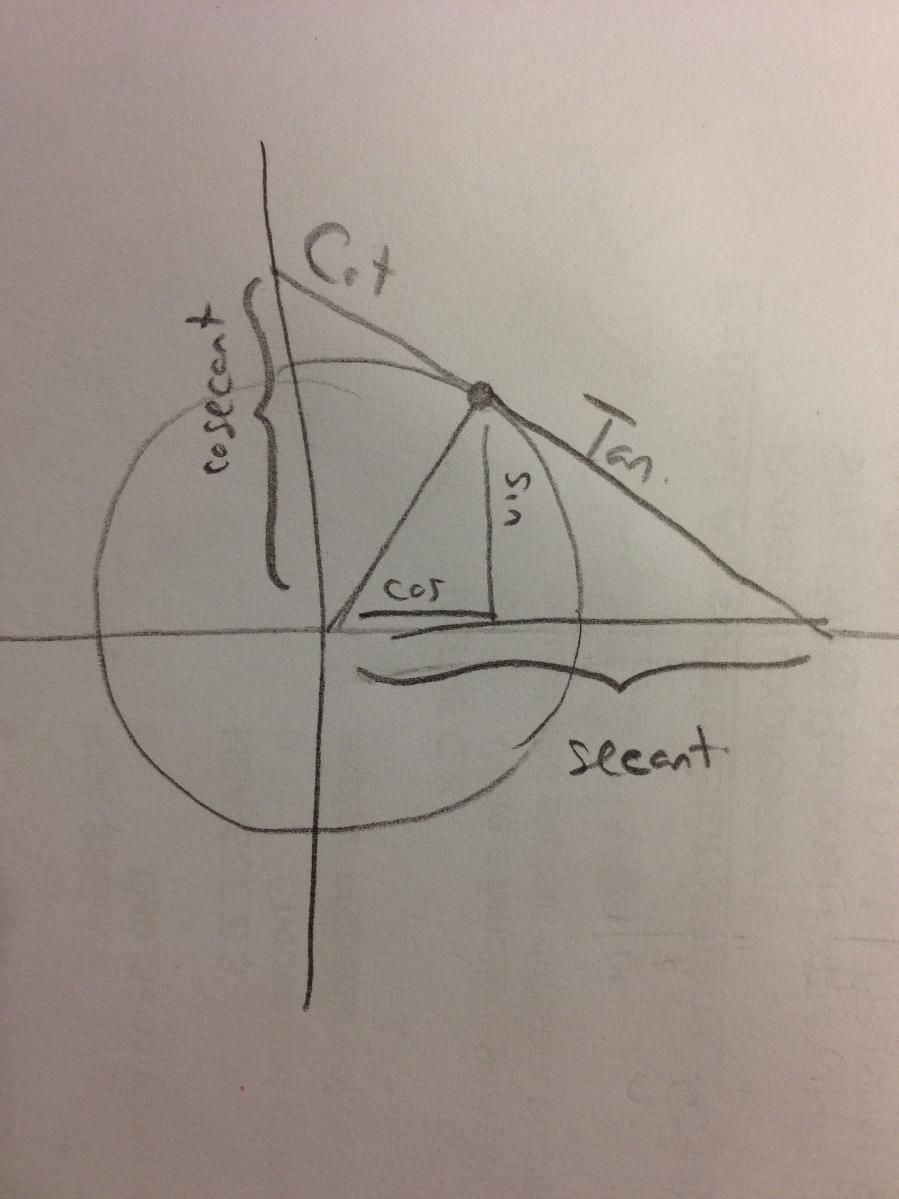
Here's some of the resulting graphs. I take pictures of some of the student work and we have a conversation about it.

Q: What do you like or dislike about this graph?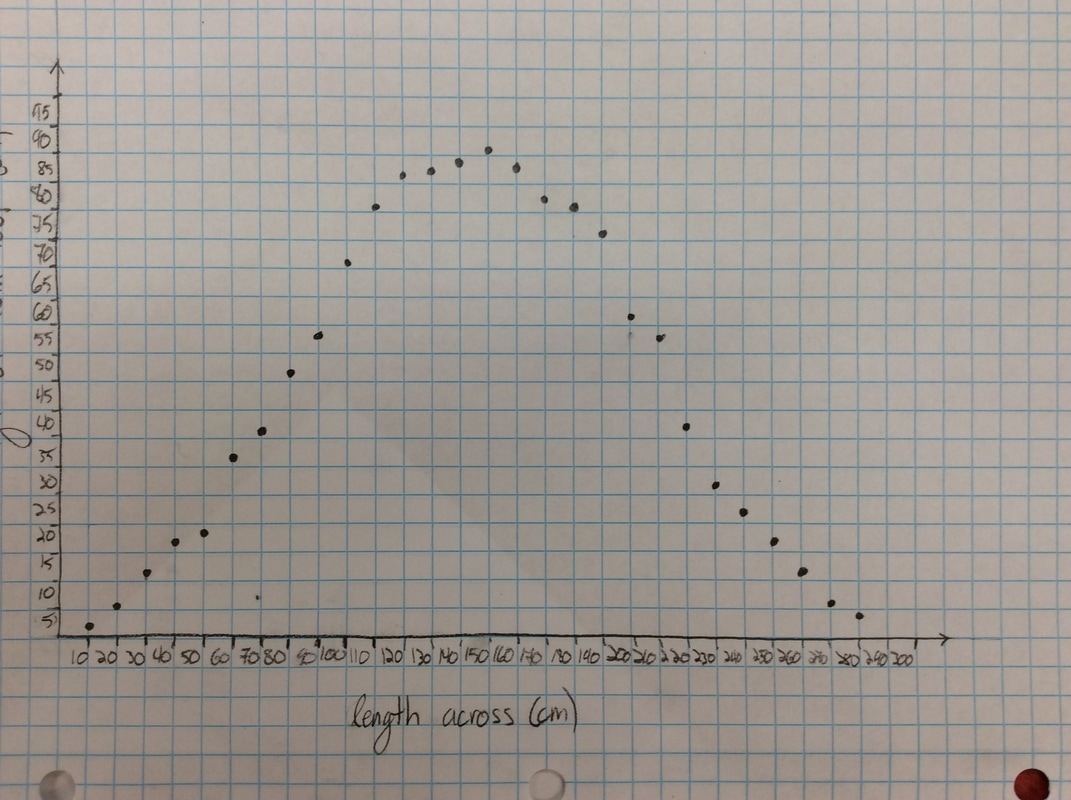

Students tend to not like the "lumpy" portions of the graph.

I put the following graph on the screen in response. Students like this one much better. As if almost on cue, some student always says we should connect the points. Then we get to have a good discussion about whether the graph should be continuous or discrete.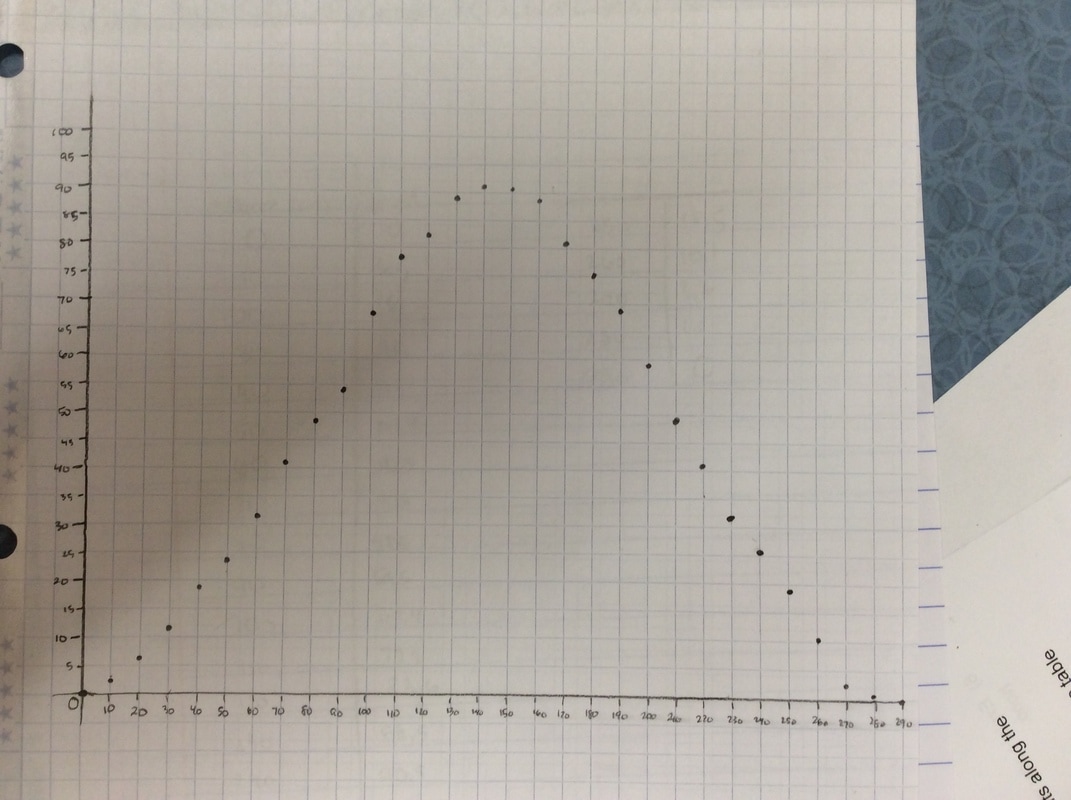

Students generally settle on the following as their "ideal" graph. We then talk about rate of change in table groups. How do you talk about rate of change with this graph? After flailing about wildly, we usually are able to give a decent explanation about whey when the point we are measuring is at the bottom or the top of the circle it doesn't have much vertical change in distance as opposed to when it is on the sides.

Day 1 usually ends here and students finish their 7 questions on the handout. This year, Day 1 was half eaten by questions over a previous assignment and we gave up half of Day 2 to finish gathering data, graphing, and having this discussion.

Day 2 begins with a discussion about the unit circle.

The following is the definition of "sine" from Wolphram Alpha. Notice the first part of the definition.

Forget the "common schoolbook definition". As a class, we define 'sine' as the vertical distance of a point on the circle to the x-axis and the 'cosine' as the horizontal distance of a point on the circle to the y-axis. It's *expletive* amazing! We talk about what this distance looks like when we move the point around the circle. Here's some of the web-based visualizations I use:
    Sine and Cosine as vertical and horizontal distances in the unit circle
        http://www.analyzemath.com/unitcircle/unit_circle_applet.html
        https://www.mathsisfun.com/algebra/trig-interactive-unit-circle.html
        https://www.desmos.com/calculator/v7x6br3w6a​
    A visualization of Sine and Cosine in the Unit Circle:
    (If you want to moving one, click on the link below)
        http://i.stack.imgur.com/p8O4P.gif

This is THE move that sets up everything! It sets up talking about sine and cosine as functions. It sets up a point on the unit circle being (cos, sin). It sets up the Law of Cosines not being some weird abnormality that's never really understood by students. It sets up that what we commonly refer to as trig ratios are lengths of lines in the unit circle. It also sets up any triangle with a hypotenuse other than 1 being a dilation of a triangle on the unit circle, with a scale factor of the length of the hypotenuse. Of course we end up deriving the shortcut methods for finding sine, cosine and tangent without having to go back to the unit circle every time. However, the fact that these are real lengths and not just abstractions goes a long way with my concrete learners. Sine is a vertical distance. Cosine is a horizontal distance. Tangent is the distance from the tangent to the point on the circle to the x-axis. Which is why tangent of 90 degrees and 270 degrees is undefined.

This also helps discuss Cotangent, Secant, and Cosecant when they come up later in the year. They are all actual lengths in the unit circle!

If you're teaching Algebra 2, after this throw in a little Cosine Ferris Wheel from MARS and you've got yourself a decent start to a trig unit.

I wrote a small Impact on Education grant this year to buy our department math toys. 

Here's a little showcase of what we've been doing:

We didn't have enough pentagons to make a dodecahedron. Students decided to fill in the gaps using triangles. 

Lots of great discussions between students. Lots of arguing. Lots of off-topic designs. Lots of on-topic designs.

Here's a lesson my brilliant colleague Tom Seibel did with his pre-algebra class:

Here's some of the things I've been doing.

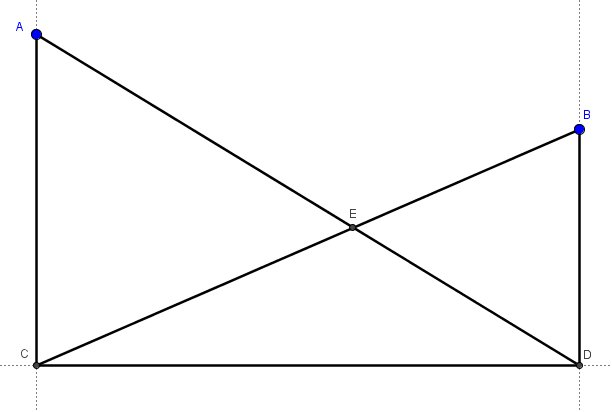
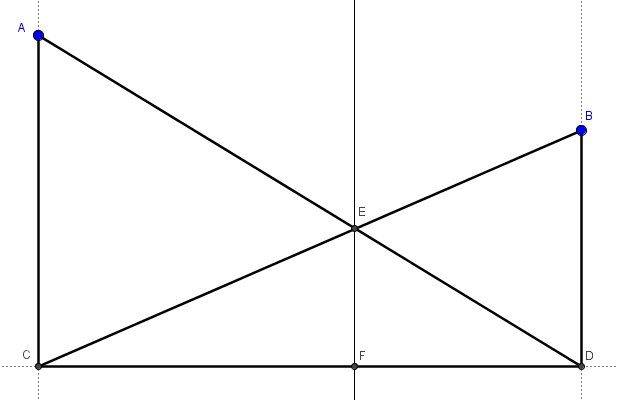
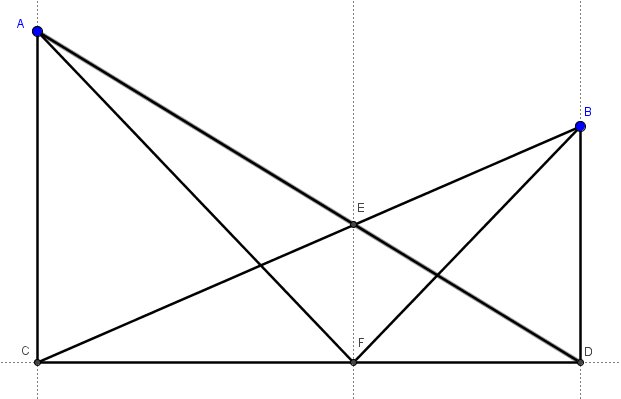
 Yesterday in class, we were doing a task made popular by Fawn Nguyen. Let's call it similar golf. Students create their own miniature golf course and then need to do a bank shot off one of the walls to get a hole in one.

I expect student solution methods to end up using similar triangles. Here's a solution method I did not expect:

Student: "Mr. Busch, I think I found a solution!"
Me: "Show me what you got."
Student: "Well, I drew perpendiculars to the wall from the Ball and the Hole.

Student: "Next, I drew the diagonals from the ball to the place where the perpendicular from the hole hit the wall. Then I drew the line from the hole to where the ball's line hits the wall."

Draw line segment AD and line segment BC. Call the intersection E.

Student: "Then from where the two diagonals intersected each other I drew another perpendicular to the wall."

Create the perpendicular from point E to line CD. Call the point of intersection F.

Student: "Where the new perpendicular hits the wall, I drew lines to the ball and the hole. This is where you should aim to make a hole in one."

Draw segment AF and segment BF.

Me: "That's really interesting. How do you know that it works?"
Student: "Well, I measured it and all the proportions check out."
Me: "Hmm. I don't know why that would be true. Can you try it with a different location of the ball and the hole and see if it still works?"
Student: "Did I just come up with something that works and you didn't know about it?!"
Me: "Maybe, but you'll need to convince me that it might be true. Maybe you just got lucky with your ball and hole placements."
Student: "Okay I'll check"

The student tried another variation and it still worked. After school, I put the situation into a Geogebra file and it does seem to hold true. At least I cant' find a counter example. So, here's the question, are triangle AFC and triangle BFD similar? Why or why not?

Here's a link to the Geogebra file I created if you want to play around with it yourself.

__EDIT__

We threw out the lesson plan in Geometry today in favor of solving this problem. Students used Geogebra to construct the situation and convince themselves of it "true-ness". Afterwards students self-clumped and went to work. Some used big-honking whiteboards. Some worked furiously in their notebooks. Good times. A couple student groups think they have a solution but the bell rang before they could write it up or present it. We'll see tomorrow. 

Behold the power of Twitter. I put the question out to the #MTBoS and got multiple responses.David Butler is the easiest to follow. And in less than 140 characters. Most impressive. 

This is the lesson I intended to use for evaluations--you know what I mean--the lesson you plan to do in the next week and a half that you think will make you look the best. Things didn't go 'terrible' but neither did we actually get to the cool part of the lesson either.  

In our study of similar figures, I use Math Assessment Project's: Floodlight Shadows. It does an excellent job progressing with a relatively simple group task (#2) involving similar triangles and then switches things up asking what happens to the length of the shadow when the football player moves (#3). The second question asks for a solution of an instance. The third question asks for a general solution method... a proof. All the resources you need are in the link. 

Okay, but we gotta back up. I have two sections of Geometry this year--3rd and 6th periods. My Principal decided to come for my second section. I'm thinking "Sweet! I'll get some practice in." I had all sorts of grand ideas about how things were going to play out. Today I need to show off my mad teaching skills. It didn't happen.

​Turns out the homework assignment from the night before ate most of my class period today. Now, in my Algebra 1B class this would have been horrid. In my Geometry class it's usually only frustrating to me--I have an agenda people!--everyone else seems cool with it.

In 3rd period, as students asked questions on problems, other students volunteered to present their solution methods. Hands were raised. Students called on each other. Mics were dropped. Laughter. Shouts. 10 minutes on the task (up through #2). Whatever, I felt brilliant.

In 6th period, I gave the students a choice, we could either go over questions at the beginning of class and have a small start on the Floodlights task or we could start the Floodlights task and go over the homework the next day. Secretly, I hoped they would choose the lesson. We put it up to a class vote and they decided to check the homework.  Okay, if things go like they did earlier in the day everything will be fine. As students asked questions on problems, ...crickets. Having them volunteer was sooo much harder than usual. Having them ask each other questions was like pulling teeth. It was akin to losing 2 months of classroom culture-building overnight. Sigh.

6th period ended their homework discussion with 15 to 20 minutes left of class. I pulled out the big honking white boards and set them to work on the task. One or two groups were ready by the time class ended but not enough for a classroom discussion. Homework was to complete task #2.

Then we upped difficulty level. What would happen to the football player's shadow when he walked towards one of the floodlights? Would the total length of both shadows stay the same or change? 

Many groups attempted to extend their previous solution method using proportions. It worked for a couple of them but there is a lot of symbolic manipulation involved. At least half the groups who tried using proportions got stuck.

The actual lesson from mathshell.org has sample solution methods for students to evaluate after they've attempted the task. Last year I used them. This year I wanted to give it a little more time. I had them printed off, just in case. I stopped the groups with 10-15 minutes left of class the second day. In both of my classes, I had one group that either didn't complete a solution method or didn't have a promising plan of how to get one.

With our last 10 minutes of class, students presented solution methods. One group had a solution so elegant they received applause from the class (6th period). They dropped the mic with wide grins. 

Homework was to revise a solution method they'd seen in class. I'm not very good at having students revise their work. I figured this was as good a time as any. We rework drafts over and over in English and History. We do experiments over and over again in science. Why not in math? I asked for complete sentences, diagrams, etc. We'll see.

Next year I'm going to split the task slide and give #3 it's own slide. Having #2 and #3 on the same page gave away too much about where I wanted to go. Some students had already attempted #3 at home the night after day 1 and controlled the discussion in their groups for too much of the time on day 2.