We began by discussing the oil spills of the Exxon Valdez (1989) and the BP Deep Water Horizon (2010). I try to be as intense and dramatic as possible. These are environmental catastrophes; I want students to feel the weight of the situation.
The BP Deep Water Horizon was the US’s largest oil spill ever. After the Deep Water drilling rig exploded--killing 11 people--the oil well continued to release oil into the ocean for another 87 days. All in all, 206 million gallons of crude oil were put into the ocean in the Summer and Fall of 2010.
However, the worst oil US spill in terms of environmental damage happened 25 years ago in 1989 when the oil tanker Exxon Valdez ran aground in waters of the Prince William Sound near the Kenai Peninsula of Alaska. An estimated 11 million gallons of oil spread on the waters and shoreline of the area, endangering wildlife. How do you begin to clean up such a mess? [students respond in all sorts of manners] How long do you thing it takes? [students again respond with very uninformed opinions].
Enter the checkers activity. I start with 80 red checkers in a tote bag and 20 black checkers representing an oil spill. I also have about 5 or 6 small bins with 20 red checkers in each for use in the activity.
Experiment (from Core-Plus Mathematics Project)
- Think about the following experiment that simulates pollution of a lake or river by some poison and the cleanup.
- Mix 20 black checkers (the pollution) with 80 red checkers (the clean water).
- On the first “day” after the spill, remove 20 checkers from the mixture (without looking at the colors) and replace them with 20 red checkers (clean water). Count the number of black checkers remaining. Then shake the new mixture. This simulates a river draining off some of the polluted water and a spring or rain adding clean water to a lake.
- On the second “day” after the spill, remove 20 checkers from the new mixture (without looking at the colors) and replace them with 20 red checkers (more clean water). Count the number of black checkers remaining. Then stir the new mixture.
- Repeat the remove/replace/mix process for several more “days”.
I ask a student to record the number of black checkers left on the whiteboard. As I go around, students take turns taking out 20 checkers. We then figure out the number of black checkers left. I let the student on the whiteboard make up his/her own organizational structure. It ends up being a decent discussion point for the class about what they like or what they would like to see in order to help understand the data better.
Sometimes the data works out really well (like in 1st period today). Sometimes it doesn't (as in 7th period today). Either way, it helps students begin to get their heads around the idea that oil is harder to clean up as the days progress. The easy oil gets cleaned up early on. The harder oil stays around for quite awhile.
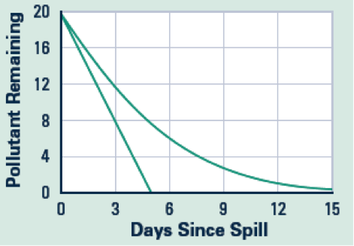
The graphs below show two possible outcomes of the pollution and cleanup simulation. I ask students about which option they think best represents the situation.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 20 | 16 | 13 | 11 | 7 | 6 | 6 |
We talk about what kind of patterns we see in the table. Every class I've ever had goes for rate of change. So we look at the differences. I'm not about to intercede at this point. After some more discussion the class comes to a consensus about the starting-value for the exponential function: a = 20. (We use the general form: y=a(b)^x).
Then I have students work in pairs to try to find the b-value. Of the 12 different groups in two different classes today, I only had 2 groups not treat the multiplier, b, like the slope. Groups had all sorts of values. They took the average difference and plugged it in for b. They took the average difference, turned it into a percent and subtracted that from 1. I could go on, but you get the idea.
Me: "What does the b-value stand for in the equation?"
Kids: "The multiplier."
Me: "Is that what you found?"
Kids: "Yes. No. We found the difference."
Me: "Is that the multiplier?"
Kids: "No."
Me: "How would you find the next y-value in the table from where we are at now?"
Kids: "You would divide 16 by 20."
Kid2: "Wait! That means we can find all the b-values and then average them."
Kids: *murmers of agreement*
Me: "You have another 3 minutes to fix your equations with your groups. Go!"
The class comes back together and we discuss the results. Then I bring up the next slide in the presentation.
This is the 25th anniversary of the ecological disaster caused by the Exxon Valdez. Unfortunately, we don't have data for this situation like we did for our experiment with the checkers. Figuring out how much oil is left involves paying people to take samples and do studies--lots of money. Now, 25 years after the fact, some people have gone back to check on the area (I have the study linked in the ppt). On the surface, things seem to be recovering well. However, when they began to look under the surface, literally, things weren't so pretty. Of the holes they dug, something like 58% of them showed visible signs of oil. It's been 25 years and things still aren't okay. They now estimate that there is still somewhere between 16 and 21 thousand gallons of oil still in the local environment. How might we go about fitting a model to this data?
In y=a(b)^x, the 'a' value is given with the 11 million gallons of oil originally spilled. We now have another point (25, ___). Every class picked a different number to use for the associated y-value. Some wanted to take the average of 16,000 and 21,000. Others wanted to use 20,000 because it was an easy number to work with. We plug in our a-value along with our point (25, 20000) and we end up with 20000 = 11000000(b)^25. Now we graph both sides of the equation to find our b-value.
The conversation then shifts back to the gulf coast. Just last month, BP was found as grossly negligent prior to the oil spill. The company faces fines up to 18 billion dollars. How do you think the Federal Judge in the case came up with the number 18 billion? How long do you think it will take to clean up?
After the lesson, several students went home and did their own voluntary research into the situation. I don't think I've ever had that happen before.
We ran out of time to talk about the ongoing disaster at the Fukushima Nuclear Power Plant. My problem ideas for that are in the attached lesson.
|
|
| ||||||
• HSF-LE.A.1
Distinguish between situations that can be modeled with linear functions and with exponential functions.
• HSF-LE.A.2
Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs
• HSF-LE.B.5
Interpret the parameters in a linear or exponential function in terms of a context.
• HSA-SSE.A.1
Interpret expressions that represent a quantity in terms of its context.★
• HSF-BF.A.1
Write a function that describes a relationship between two quantities.★
• HSF-BF.A.2
Write arithmetic and geometric sequences both recursively and with an explicit formula, use them to model situations, and translate between the two forms.★
 RSS Feed
RSS Feed



