We still need work out the details regarding what the essential learning targets are and how we will build space into the schedule for re-assessment. We plan to do that this Thursday.
This is a big deal. We’re making a structural shift in how we, as a team, plan for units and how we grade student learning in “regular” math classes. We’ve already moved towards a modified standards-based grading as an Algebra 2 team this year. Kudos to the team for being willing to take the plunge deeper into grading for student learning.
Here’s to all of our students passing Algebra 2!























































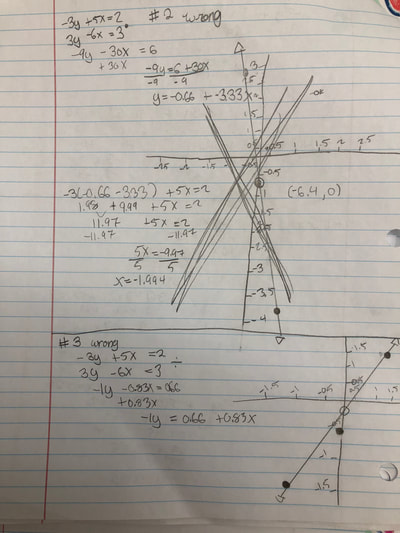

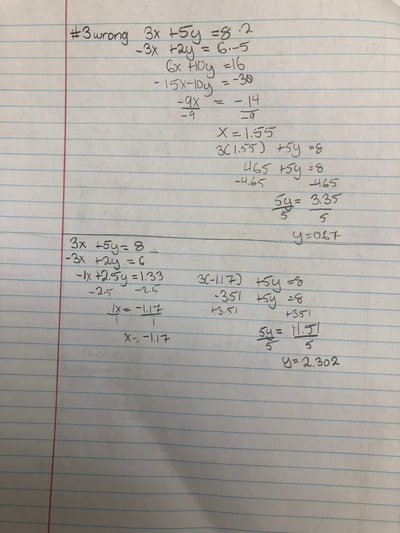

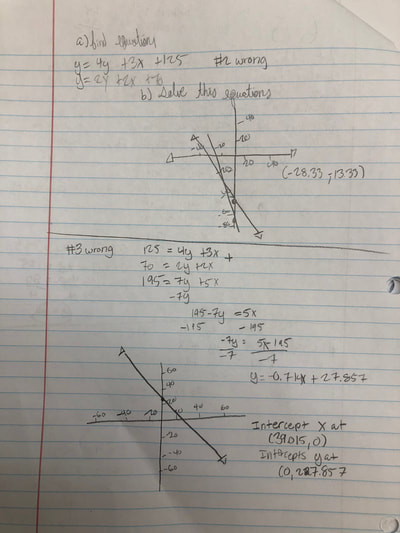
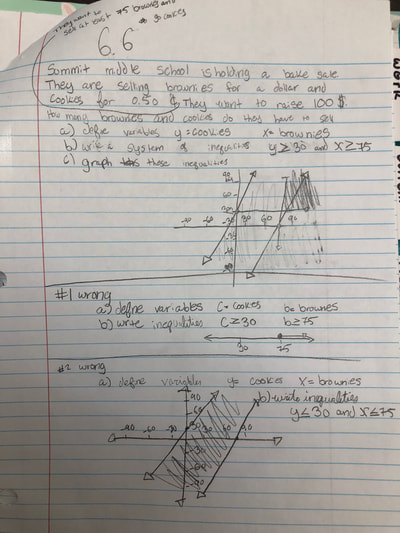

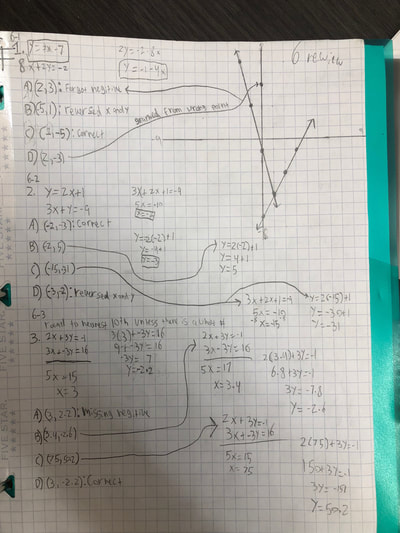

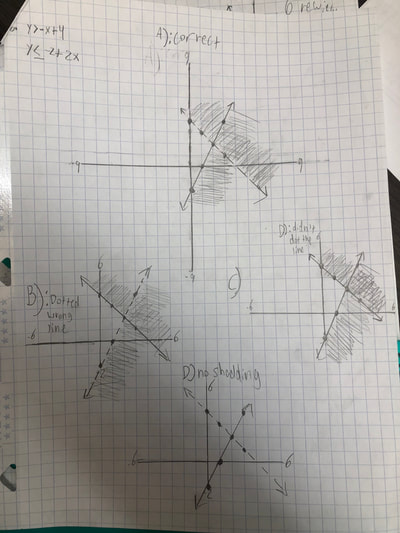
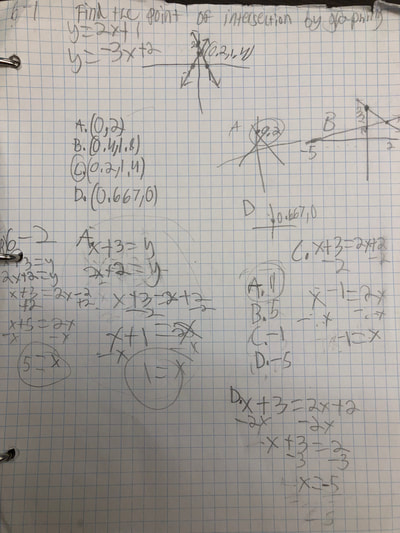

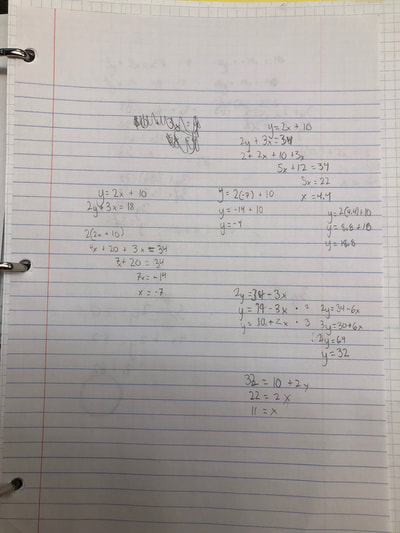
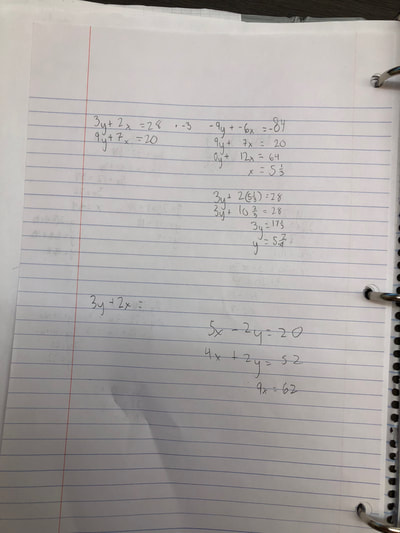





 RSS Feed
RSS Feed



