|
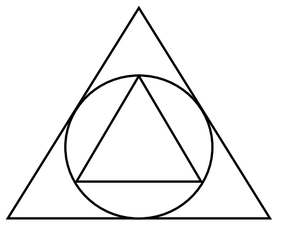
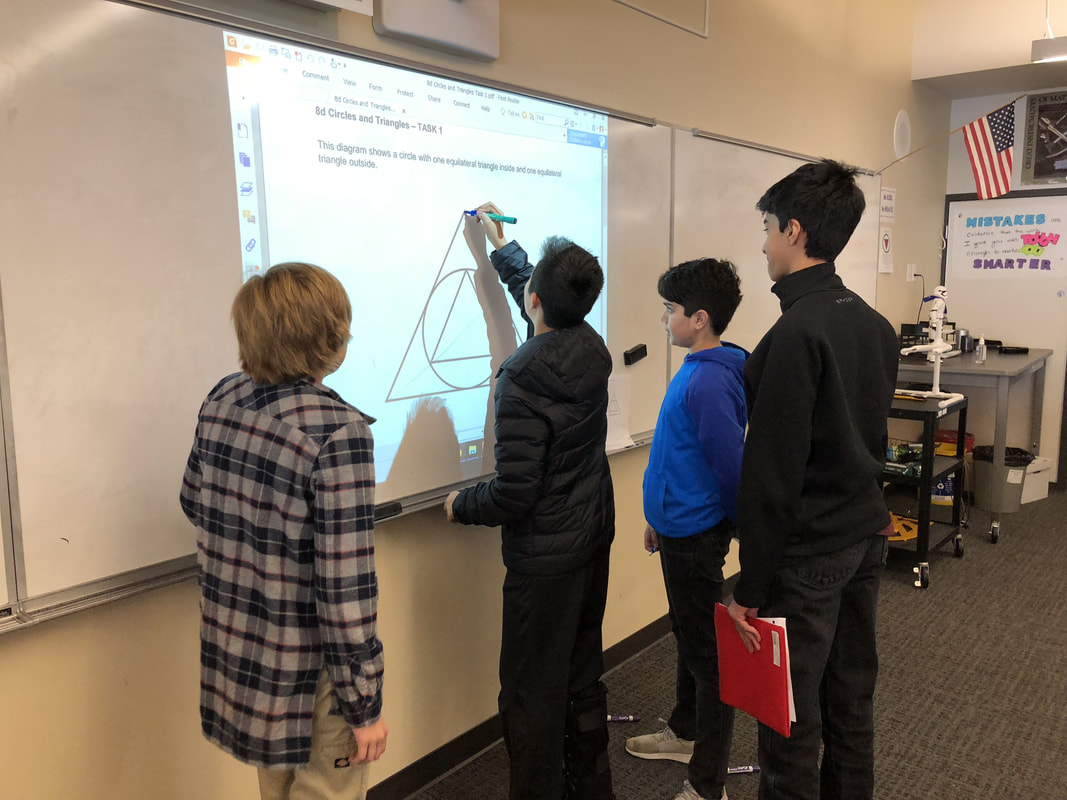
We spent a day working on a fun task from the MARS Team. Here is the only setup:
After spending 30 minutes or so working on this problem in groups, we ran out of time. Meh. We planned on starting class the next day talking about our ideas for solution methods. Normally, with two minutes left of class, they line up at the door like cattle. Some of the students weren't done with the problem yet. I didn't do a very good job posting about activities as I did them this year. I'm working through a new Algebra 1 curriculum (I'm not impressed with it) and I'm trying to rethink how I do formative assessment. My activities aren't changing much this year, the amount of time we spend doing activities and experiments feels about right. I guess that's a good thing. Here's an activity we do at the beginning of our unit on linearity: cup stacking. I took this idea hook line and sinker from Dan Meyer and Andrew Stadel. Rather than do this as a 3 ACT lesson, I use it as a chance to get students out of their seats and talking to one another.
We begin by giving 5 styrofoam cups to every pair of students. Then I show a picture of me getting my height measured at my doctor's office (in cm). They have to figure out how many cups tall I am. We also almost always need to come to an agreement about how to measure the cups. Quick setup and clean up and almost complete engagement. You can't ask for much more than that. This activity helps students solidify their understanding of the new vocabulary identifying the angles created by a transversal between two lines. To make it a wee-bit more interesting, we also look at transversals across non-parallel lines. I'm struggling to find time to write thoughtful posts. But I am taking pictures. Here's some fun shots of our Ball Drop experiment in Algebra 1.
|
Andrew Busch
I teach Math at Ralston Valley High School in Arvada, CO. Categories
All
Archives
March 2019
|







































































 RSS Feed
RSS Feed



